Review Số ảo python

Thủ Thuật Hướng dẫn Số ảo python Mới Nhất

Lê Thùy Chi đang tìm kiếm từ khóa Số ảo python được Cập Nhật vào lúc : 2022-12-19 05:38:03 . Với phương châm chia sẻ Bí kíp về trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi tham khảo Post vẫn ko hiểu thì hoàn toàn có thể lại Comments ở cuối bài để Admin lý giải và hướng dẫn lại nha.

Chúng ta sẽ cùng nhau tìm làm rõ ràng hơn về những kiểu số trong Python gồm có. Số nguyên (int), số thực (float), số phức (Phức). Đồng thời tất cả chúng ta cũng tiếp tục tìm hiểu về những hàm, những phép toán thông thường được sử dụng với những kiểu số

Nội dung chính Show

Giới thiệu chung về những kiểu số trong Pythoninteger type (int)Kiểu số thực (float)Các kiểu số phức (Phức tạp)Tạo số phức trong PythonSố Phức Chữ>>> type(z) 11 Chức năng nhà máyLàm quen với số phức PythonTruy cập phần thực và phần ảoTính phối hợp của một số trong những phứcSố phức Số họcPhép cộngphép trừPhép nhânPhân cônglũy thừaSử dụng số phức Python làm vectơ 2DLấy tọa độTính độ lớnTìm Khoảng Cách Giữa Hai ĐiểmDịch, lật, thu nhỏ và xoayKhám phá mô-đun toán học về số phức. >>> z = 3.14 + 0j >>> type(z) 9Trích xuất gốc của một số trong những phứcChuyển đổi giữa tọa độ hình chữ nhật và cựcBiểu diễn số phức theo cách khácPhân tích một số trong những phức trong PythonKiểm tra đẳng thức của số phứcSắp xếp những số phứcĐịnh dạng số phức dưới dạng chuỗiTạo kiểu tài liệu phức tạp của riêng bạnTính phép biến hóa Fourier rời rạc với số phứcPhần kết luận

Nội dung của nội dung bài viết

Giới thiệu chung về những kiểu số trong Python

Kiểu số là kiểu cơ bản trong những ngôn từ lập trình, Python tương hỗ 3 kiểu số là số nguyên (int), số thực (float), số phức (phức tạp). Kiểu số trong Python is Immutable (không bao giờ thay đổi), tức là lúc tất cả chúng ta gán biến num cho một value is number thì giá trị đó không thay đổi sau đó. Khi chúng tôi gán cho biến số giá trị khác trên thực tế, trình thông dịch sẽ khởi động tạo giá trị mới và trỏ biến số địa mới chỉ này

Dựa vào cách khai làm giá trị mà Python sẽ tự động nhận ra kiểu của những số. Ví dụ. num = 100, the transaction information will start a memory chứa integer, pi = 3. 14 thì sẽ khởi động số thực, comp = 10j sẽ khởi động số phức

Python có nhiều thư viện tương hỗ những hàm học, những phép tính. Có thể vì hiệp hội sử dụng Python xử lý những bài toán liên quan đến tài liệu lớn, ML. Tất nhiên Python tương hỗ những phép tính cơ bản như +, -, sin, cos…

integer type (int)

Số nguyên (int) trong Python không số lượng giới hạn độ dài và được màn biểu diễn dưới dạng số nguyên dương, số nguyên âm, số ở dạng thập phân, hệ cơ số 8 và hệ cơ số 16

Khi màn biểu diễn ở hệ cơ số 8 tất cả chúng ta sử dụng tiếp tục 0o hoặc 0O (số 0 và vần âm o hoa, thường. ồ)

Khi màn biểu diễn số ở hệ cơ số 16 ta sử dụng tiếp tục 0x hoặc 0X (số 0 và vần âm x hoa, thường. XX)

Ví dụ

Giá trị Mô tả10Số nguyên dương-100Số nguyên âm0o400Số nguyên dương cơ số 8 (là số nguyên 256 ở cơ số 10)-0o400Số nguyên âm cơ số 8(là số -256 cơ số 10)0x100Số nguyên dương cơ số 16(là số nguyên

Kiểu số thực (float)

Float trong python in như ở những ngôn từ khác, sử dụng để biểu thị số thực hiện dấu phẩy động. Có thể viết rút gọn bằng phương pháp sử dụng ký tự e kèm theo số phía sau, ví dụ. e2 tương đương với 10 mũ 2 (10^2)

The valueMô tả10. 0 hoặc 10. Số thực dương 10. 0-100. 0Số thực âm100e2= 100 * 10^2 == 10000. 0-100e-2= -100 * 10^-2 == -1. 00x100Số nguyên dương cơ số 16 (là số nguyên 256 ở cơ số 10)-0x100Số nguyên âm cơ số 16 (là số -256 cơ số 10)

Các kiểu số phức (Phức tạp)

Python tương hỗ trực tiếp những kiểu số phức, đơn vị ảo được biểu thị bởi ký tự j hoặc J (trong toán học là i), j hoặc J phải đi kèm với số nếu không xem là một biến

Hầu hết những ngôn từ lập trình có mục tiêu chung đều không tương hỗ hoặc tương hỗ hạn chế cho những số phức. Các tùy chọn điển hình của bạn là học một số trong những công cụ chuyên được dùng như MATLAB hoặc tìm thư viện của bên thứ ba. Python là một ngoại lệ khan hiếm vì nó đi kèm với những số phức được tích hợp sẵn

Mặc dù tên, số phức không phức tạp. Chúng thuận tiện trong việc xử lý và xử lý những vấn đề thực tế mà bạn sẽ cảm nhận được trong hướng dẫn này. Bạn sẽ mày mò đồ họa vector và phân tích tần số âm thanh, nhưng những số phức cũng hoàn toàn có thể giúp vẽ những fractal, ví dụ như tập hợp Mandelbrot

Trong hướng dẫn này, bạn sẽ học cách

Xác định số phức bằng chữ trong PythonBiểu diễn những số phức trong hệ tọa độ vuông góc và cựcSử dụng số phức trong biểu thức số họcTận dụng mô-đun >>> z = 3.14 + 0j >>> type(z) 9 tích hợpDịch những công thức toán học trực tiếp sang mã Python

Nếu bạn cần xem lại nhanh hoặc ra mắt nhẹ nhàng về lý thuyết số phức, thì bạn hoàn toàn có thể xem loạt video của Khan Academy. Để tải xuống mã mẫu được sử dụng trong hướng dẫn này, hãy nhấp vào link phía dưới

Nhận mã mẫu. Nhấp vào đây để lấy mã mẫu mà bạn sẽ sử dụng để tìm hiểu về số phức trong Python trong hướng dẫn này

Tạo số phức trong Python

Tạo và thao tác với những số phức trong Python không khác nhiều so với những kiểu tài liệu dựng sẵn khác, đặc biệt là những kiểu số. Có thể vì ngôn từ coi họ là công dân hạng nhất. Điều này nghĩa là bạn hoàn toàn có thể diễn đạt những công thức toán học liên quan đến những số phức với ít ngân sách

Python được cho phép bạn sử dụng những số phức trong những biểu thức số học và gọi những hàm trên chúng in như cách bạn làm với những số khác trong Python. Nó dẫn đến cú pháp tao nhã gần in như một cuốn sách giáo khoa toán học

Loại bỏ những quảng cáo

Số Phức Chữ

Cách nhanh nhất có thể để xác định một số trong những phức trong Python là gõ trực tiếp chữ của nó vào mã nguồn

>>>

>>> z = 3 + 2j

Mặc dù điều này trông in như một công thức đại số, nhưng biểu thức ở bên phải của dấu bằng đã là một giá trị cố định và thắt chặt không cần đánh giá thêm. Khi bạn kiểm tra loại của nó, bạn sẽ xác nhận rằng đó thực sự là một số trong những phức

>>>

>>> type(z)

Điều đó khác với phép cộng hai số bằng toán tử cộng ra làm sao? . Nếu bạn xóa vần âm, thay vào đó, bạn sẽ nhận được kết quả số nguyên quen thuộc

>>>

>>> z = 3 + 2 >>> type(z)

Nhân tiện, bạn cũng hoàn toàn có thể sử dụng số dấu phẩy động để tạo số phức

>>>

>>> z = 3.14 + 2.71j >>> type(z)

Chữ số phức trong Python bắt chước ký hiệu toán học, còn được gọi là dạng chuẩn, dạng đại số hoặc đôi khi là dạng chính tắc của một số trong những phức. Trong Python, bạn hoàn toàn có thể sử dụng chữ thường

>>> 2 + 3j + 4 + 5j (6+8j) 0 hoặc chữ hoa >>> 2 + 3j + 4 + 5j (6+8j) 2 trong những chữ đó

Nếu bạn đã học về số phức trong lớp toán, bạn hoàn toàn có thể đã thấy chúng được biểu thị bằng phương pháp sử dụng

>>> 2 + 3j + 4 + 5j (6+8j) 3 thay vì >>> 2 + 3j + 4 + 5j (6+8j) 0. Nếu bạn tò mò về nguyên do Python sử dụng >>> 2 + 3j + 4 + 5j (6+8j) 0 thay vì >>> 2 + 3j + 4 + 5j (6+8j) 3, thì bạn hoàn toàn có thể mở rộng phần hoàn toàn có thể thu gọn phía dưới để tìm hiểu thêm

Tại sao lại là >>> 2 + 3j + 4 + 5j (6+8j) 0 thay vì >>> 2 + 3j + 4 + 5j (6+8j) 3?Hiển thị/Ẩn

Ký hiệu truyền thống cho những số phức sử dụng vần âm

>>> 2 + 3j + 4 + 5j (6+8j) 3 thay vì >>> 2 + 3j + 4 + 5j (6+8j) 0 vì nó là viết tắt của đơn vị ảo. Bạn hoàn toàn có thể cảm thấy hơi rất khó chịu với quy ước của Python nếu bạn có nền tảng toán học. Tuy nhiên, có một vài nguyên do hoàn toàn có thể biện minh cho việc lựa chọn gây tranh cãi của Python

Đó là một quy ước đã được những kỹ sư áp dụng để tránh xung đột tên với dòng điện, được ký hiệu bằng vần âm >>> 2 + 3j + 4 + 5j (6+8j) 3Trong điện toán, vần âm >>> 2 + 3j + 4 + 5j (6+8j) 3 thường được sử dụng cho biến chỉ mục trong những vòng lặpChữ cái >>> 2 + 3j + 4 + 5j (6+8j) 3 hoàn toàn có thể dễ bị nhầm lẫn với >>> type(z) 04 hoặc >>> type(z) 05 trong mã nguồn

Điều này đã được đưa ra trên trình theo dõi lỗi của Python hơn một thập kỷ trước và chính người tạo ra Python, Guido van Rossum, đã đóng vấn đề bằng nhận xét này

Điều này sẽ không được sửa chữa. Đối với một điều, chữ 'i' hoặc chữ hoa 'I' trông quá giống những chữ số. Cách những số được phân tích cú pháp bằng trình phân tích cú pháp ngôn từ (trong mã nguồn) hoặc bằng những hàm dựng sẵn (int, float, complex) không được bản địa hóa hoặc hoàn toàn có thể định thông số kỹ thuật theo bất kỳ cách nào; . Nếu bạn muốn phân tích những số phức bằng phương pháp sử dụng 'i' thay vì 'j', bạn đã có sẵn rất nhiều giải pháp. ()

Vì vậy, có bạn có nó. Trừ khi bạn muốn khởi đầu sử dụng MATLAB, nếu không bạn sẽ phải sống với việc sử dụng

>>> 2 + 3j + 4 + 5j (6+8j) 0 để biểu thị những số phức của tớ

Dạng đại số của số phức tuân theo những quy tắc chuẩn của đại số, thuận tiện khi thực hiện những phép tính số học. Ví dụ, phép cộng có thuộc tính giao hoán, được cho phép bạn hoán đổi thứ tự của hai phần của một số trong những phức bằng chữ mà không làm thay đổi giá trị của nó

>>>

>>> type(z) 2

Tương tự, bạn hoàn toàn có thể thay thế phép cộng bằng phép trừ trong một số trong những phức bằng chữ vì dấu trừ chỉ là ký hiệu viết tắt cho một dạng tương đương

>>>

>>> type(z) 3

Có phải một số trong những phức bằng chữ trong Python luôn phải gồm có hai số không? . Không ngạc nhiên, nếu bạn chỉ xác định một số trong những, không còn vần âm

>>> 2 + 3j + 4 + 5j (6+8j) 0, thì bạn sẽ nhận được một số trong những nguyên thông thường hoặc một số trong những dấu phẩy động

>>>

>>> type(z) 5

Mặt khác, thêm vần âm

>>> 2 + 3j + 4 + 5j (6+8j) 0 vào một chữ số sẽ ngay lập tức biến nó thành một số trong những phức

>>>

>>> type(z) 7

Nói một cách đúng chuẩn, từ quan điểm toán học, bạn vừa tạo một số trong những ảo thuần túy, nhưng Python không thể màn biểu diễn nó dưới dạng một kiểu tài liệu độc lập. Do đó, không còn phần còn sót lại, nó chỉ là một số trong những phức

Còn ngược lại thì sao?

>>>

>>> z = 3.14 + 0j >>> type(z)

Thật vậy, cả hai phần của số phức luôn có. Khi bạn không nhìn thấy một, điều đó nghĩa là nó có mức giá trị bằng không. Hãy kiểm tra xem điều gì sẽ xảy ra khi bạn nỗ lực thêm nhiều số hạng vào tổng hơn trước đây đây

>>>

>>> 2 + 3j + 4 + 5j (6+8j)

Lần này, biểu thức của bạn không hề là một chữ vì Python đã đánh giá nó thành một số trong những phức chỉ gồm có hai phần. Hãy nhớ rằng những quy tắc cơ bản của đại số áp dụng cho những số phức, vì vậy nếu bạn nhóm những số hạng tương tự nhau và áp dụng phép cộng thành phần, thì bạn sẽ có kết quả là ________ 209

Lưu ý cách Python hiển thị những số phức theo mặc định. Biểu diễn văn bản của chúng chứa một cặp dấu ngoặc đơn kèm theo, một vần âm viết thường

>>> 2 + 3j + 4 + 5j (6+8j) 0 và không còn tầm khoảng chừng trắng. Ngoài ra, phần tưởng tượng đến thứ hai

Các số phức cũng là số ảo thuần túy xuất hiện mà không còn dấu ngoặc đơn và chỉ tiết lộ phần ảo của chúng

>>>

>>> type(z) 0

Điều này giúp phân biệt những số ảo với hầu hết những số phức được tạo thành từ phần thực và phần ảo

Loại bỏ những quảng cáo

>>> type(z) 11 Chức năng nhà máy sản xuất

Python có một hàm tích hợp sẵn,

>>> type(z) 11, mà bạn hoàn toàn có thể sử dụng thay thế cho chữ số phức

>>>

>>> type(z) 1

Ở dạng này, nó in như một bộ hoặc một cặp số thông thường được sắp xếp theo thứ tự. Sự tương tự không thật xa vời. Các số phức có cách diễn giải hình học trong hệ tọa độ Descartes mà bạn sẽ mày mò sau. Bạn hoàn toàn có thể coi số phức là hai chiều

Sự thật thú vị. Trong toán học, những số phức thường được biểu thị bằng vần âm

>>> type(z) 13 vì đây là vần âm tiếp theo trong bảng vần âm sau >>> type(z) 14 và >>> type(z) 15, thường biểu thị những tọa độ

Hàm nhà máy sản xuất số phức đồng ý hai tham số số. Cái đầu tiên đại diện cho phần thực, trong khi cái thứ hai đại diện cho phần ảo được biểu thị bằng vần âm

>>> 2 + 3j + 4 + 5j (6+8j) 0 trong chữ mà bạn đã thấy trước đó

>>>

>>> type(z) 2

Cả hai tham số đều là tùy chọn, với những giá trị mặc định bằng 0, giúp việc xác định những số phức không còn phần ảo hoặc cả phần thực và phần ảo trở nên thuận tiện và đơn giản hơn

>>>

>>> type(z) 3

Phiên bản một đối số hoàn toàn có thể hữu ích trong việc truyền kiểu. Ví dụ: bạn hoàn toàn có thể chuyển một giá trị không phải là số như một chuỗi ký tự để nhận đối tượng ________ 217 tương ứng. Tuy nhiên, lưu ý rằng chuỗi không được chứa bất kỳ khoảng chừng trắng nào

>>>

>>> type(z) 4

Sau này, bạn sẽ tìm hiểu cách làm cho những lớp của tớ tương thích với cơ chế truyền kiểu này. Thật thú vị, khi bạn chuyển một số trong những phức cho

>>> type(z) 11, bạn sẽ nhận lại được cùng một ví dụ

>>>

>>> type(z) 5

Điều đó phù phù phù hợp với phương pháp hoạt động và sinh hoạt giải trí của nhiều chủng loại số khác trong Python vì tất cả chúng đều không thay đổi. Để tạo một bản sao khác lạ của một số trong những phức, bạn phải gọi lại hàm có cả hai đối số hoặc khai báo một biến khác có chữ số phức

>>>

>>> type(z) 6

Khi bạn đáp ứng hai đối số cho hàm, chúng phải luôn là số, ví dụ như

>>> type(z) 19, >>> type(z) 20 hoặc >>> type(z) 17. Nếu không, bạn sẽ gặp lỗi thời gian chạy. Về mặt kỹ thuật, >>> type(z) 22 là một phân lớp của >>> type(z) 19, vì vậy nó cũng tiếp tục hoạt động và sinh hoạt giải trí

>>>

>>> type(z) 7

Mọi thứ dường như trở nên kỳ lạ hơn khi bạn đáp ứng hàm xuất xưởng

>>> type(z) 11 với những số phức làm đối số. Tuy nhiên, nếu bạn chỉ đáp ứng đối số đầu tiên, nó sẽ hoạt động và sinh hoạt giải trí in như một proxy như trước đây

>>>

>>> type(z) 8

Tuy nhiên, khi có hai đối số và ít nhất một trong số chúng là số phức, bạn sẽ nhận được kết quả hoàn toàn có thể khó lý giải ngay từ cái nhìn đầu tiên

>>>

>>> type(z) 9

Để có câu vấn đáp, hãy xem qua chuỗi tài liệu của hiệu suất cao xuất xưởng hoặc tài liệu trực tuyến, lý giải điều gì đang ra mắt khi bạn gọi

>>> type(z) 25

Trả về một số trong những phức với giá trị thực + hình ảnh*1j hoặc quy đổi một chuỗi hoặc số thành một số trong những phức. ()

Trong phần lý giải này,

>>> type(z) 26 và >>> type(z) 27 là tên gọi của những đối số hàm. Đối số thứ hai được nhân với đơn vị ảo >>> 2 + 3j + 4 + 5j (6+8j) 0 và kết quả được thêm vào đối số đầu tiên. Đừng lo ngại nếu nó vẫn không còn ý nghĩa gì. Bạn hoàn toàn có thể quay lại phần này khi bạn đã đọc về. Các quy tắc mà bạn sẽ tìm hiểu sẽ làm cho điều này trở nên đơn giản

Khi nào bạn muốn sử dụng hiệu suất cao nhà máy sản xuất

>>> type(z) 11 theo nghĩa đen?

Loại bỏ những quảng cáo

Làm quen với số phức Python

Trong toán học, số phức là tập hợp siêu của những số thực, nghĩa là mọi số thực cũng là số phức có phần ảo bằng 0. Python quy mô hóa quan hệ này thông qua một khái niệm gọi là tháp số, được mô tả trong PEP 3141

>>>

>>> z = 3 + 2 >>> type(z) 0

Mô-đun

>>> type(z) 30 tích hợp xác định khối mạng lưới hệ thống phân cấp nhiều chủng loại số thông qua những lớp trừu tượng hoàn toàn có thể được sử dụng để kiểm tra loại và phân loại số. Ví dụ: để xác định xem một giá trị có thuộc về một tập hợp số rõ ràng hay là không, bạn hoàn toàn có thể gọi >>> type(z) 31 trên đó

>>>

>>> z = 3 + 2 >>> type(z) 1

Giá trị dấu phẩy động

>>> type(z) 32 là một số trong những thực cũng là một số trong những phức nhưng không phải là một số trong những nguyên. Lưu ý rằng bạn không thể sử dụng nhiều chủng loại tích hợp trực tiếp trong thử nghiệm như vậy

>>>

>>> z = 3 + 2 >>> type(z) 2

Sự khác lạ giữa

>>> type(z) 17 và >>> type(z) 34 là chúng thuộc về những nhánh riêng biệt trong cây phân cấp kiểu số và cái sau là lớp cơ sở trừu tượng không còn bất kỳ triển khai nàoNhập phân cấp cho những số trong Python

Các lớp cơ sở trừu tượng, được biểu thị bằng red color trong sơ đồ trên, hoàn toàn có thể bỏ qua cơ chế kiểm tra thừa kế thông thường bởi những lớp không liên quan như những lớp con ảo của chúng. Đó là nguyên do tại sao một giá trị dấu chấm động trong ví dụ dường như thể một thể hiện của

>>> type(z) 34 nhưng không phải là >>> type(z) 17

Truy cập phần thực và phần ảo

Để lấy phần thực và phần ảo của một số trong những phức trong Python, bạn hoàn toàn có thể sử dụng những thuộc tính

>>> type(z) 37 và >>> type(z) 38 tương ứng

>>>

>>> z = 3 + 2 >>> type(z) 3

Cả hai thuộc tính đều ở dạng chỉ đọc vì số phức là không bao giờ thay đổi, do đó, việc nỗ lực gán một giá trị mới cho một trong số chúng sẽ không thành công

>>>

>>> z = 3 + 2 >>> type(z) 4

Vì mọi số trong Python là một loại số phức rõ ràng hơn, nên những thuộc tính và phương thức được xác định trong

>>> type(z) 34 cũng luôn có thể có sẵn trong tất cả nhiều chủng loại số, gồm có >>> type(z) 19 và >>> type(z) 20

>>>

>>> z = 3 + 2 >>> type(z) 5

Phần ảo của những số lượng như vậy luôn bằng không

Tính phối hợp của một số trong những phức

Số phức Python chỉ có ba thành viên công khai minh bạch. Ngoài những thuộc tính

>>> type(z) 37 và >>> type(z) 38, chúng còn đưa ra phương thức >>> type(z) 44, lật dấu của phần ảo

>>>

>>> z = 3 + 2 >>> type(z) 6

Đối với những số có phần ảo bằng 0, nó sẽ không còn công dụng gì

>>>

>>> z = 3 + 2 >>> type(z) 7

Hoạt động này là nghịch đảo của nó, vì vậy gọi nó hai lần sẽ giúp bạn đã có được số ban đầu mà bạn đã khởi đầu

>>>

>>> z = 3 + 2 >>> type(z) 8

Mặc dù có vẻ như ít giá trị, nhưng phối hợp phức có một số trong những tính chất số học hữu ích hoàn toàn có thể giúp tính toán phép chia hai số phức bằng bút và giấy, trong số nhiều thứ khác

Loại bỏ những quảng cáo

Số phức Số học

Vì

>>> type(z) 17 là một kiểu tài liệu gốc trong Python, nên bạn hoàn toàn có thể cắm những số phức vào những biểu thức số học và gọi nhiều hàm tích hợp trên chúng. Các hàm nâng cao hơn cho số phức được định nghĩa trong mô-đun >>> z = 3.14 + 0j >>> type(z) 9, là một phần của thư viện chuẩn. Bạn sẽ được ra mắt về nó trong phần sau của hướng dẫn này

Hiện tại, việc ghi nhớ một quy tắc duy nhất sẽ được cho phép bạn áp dụng kiến ​​thức số học ở trường tiểu học để tính toán những phép tính cơ bản liên quan đến số phức. Quy tắc cần nhớ là định nghĩa của đơn vị ảo, thỏa mãn phương trình sau

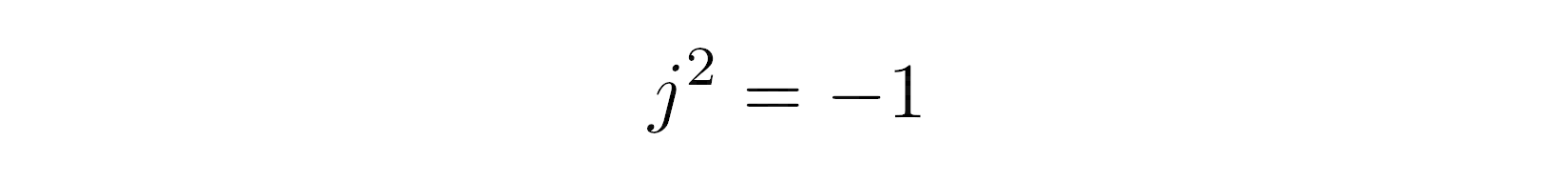
Có vẻ không đúng khi bạn coi _______ 30 là một số trong những thực, nhưng đừng hoảng sợ. Nếu bạn bỏ qua nó trong giây lát và thay thế mọi lần xuất hiện của

>>> 2 + 3j + 4 + 5j (6+8j) 0>>> type(z) 49 bằng >>> type(z) 50 như thể nó là một hằng số, thì bạn sẽ bị mắc kẹt. Hãy xem nó hoạt động và sinh hoạt giải trí ra làm sao

Phép cộng

Tổng của hai hoặc nhiều số phức tương đương với việc cộng những phần thực và phần ảo của chúng theo từng thành phần

>>>

>>> z = 3 + 2 >>> type(z) 9

Trước đó, bạn đã biết rằng những biểu thức đại số gồm có những số thực và số ảo tuân theo những quy tắc chuẩn của đại số. Khi bạn viết nó ra dưới dạng đại số, bạn sẽ hoàn toàn có thể áp dụng thuộc tính phân phối và đơn giản hóa công thức bằng phương pháp vô hiệu và nhóm những thuật ngữ phổ biến

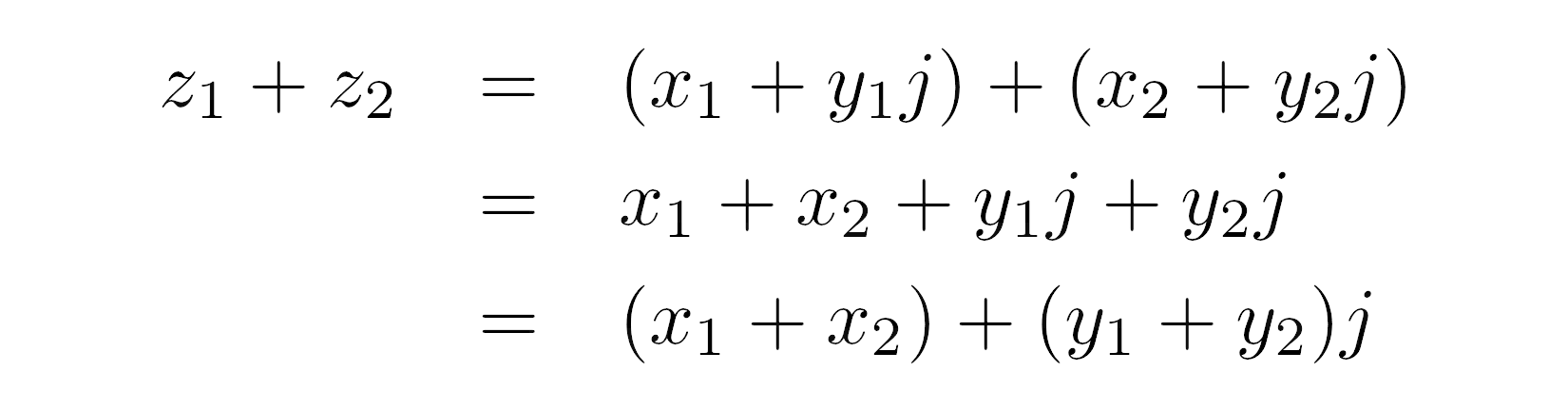
Python tự động thăng cấp toán hạng cho kiểu tài liệu

>>> type(z) 17 khi bạn thêm giá trị của những kiểu số hỗn hợp

>>>

>>> z = 3.14 + 2.71j >>> type(z) 0

Điều đó tương tự với việc quy đổi ngầm định từ

>>> type(z) 19 sang >>> type(z) 20 mà bạn hoàn toàn có thể quen thuộc hơn

phép trừ

Trừ những số phức cũng tương tự như cộng chúng, nghĩa là bạn cũng hoàn toàn có thể áp dụng nó theo từng phần tử

>>>

>>> z = 3.14 + 2.71j >>> type(z) 1

Tuy nhiên, không in như tổng, thứ tự của những toán hạng là quan trọng và mang lại những kết quả khác in như với số thực

>>>

>>> z = 3.14 + 2.71j >>> type(z) 2

Bạn cũng hoàn toàn có thể sử dụng toán tử trừ một ngôi (-) để tạo thành số âm của một số trong những phức

>>>

>>> z = 3.14 + 2.71j >>> type(z) 3

Điều này đảo ngược cả phần thực và phần ảo của số phức

Loại bỏ những quảng cáo

Phép nhân

Tích của hai hay nhiều số phức trở nên thú vị hơn

>>>

>>> z = 3.14 + 2.71j >>> type(z) 4

Làm thế quái nào mà bạn lại kết thúc với một số trong những âm trong số những số dương duy nhất?

Quan sát quan trọng cần thực hiện là

>>> 2 + 3j + 4 + 5j (6+8j) 0 nhân với >>> 2 + 3j + 4 + 5j (6+8j) 0 cho >>> 2 + 3j + 4 + 5j (6+8j) 0>>> type(z) 49, hoàn toàn có thể thay thế bằng >>> type(z) 50. Điều này đảo ngược tín hiệu của một trong những triệu hồi, trong khi phần còn sót lại của những quy tắc vẫn in như trước đây

Phân công

Việc chia những số phức hoàn toàn có thể trông đáng sợ ngay từ lần gặp đầu tiên

>>>

>>> z = 3.14 + 2.71j >>> type(z) 5

Dù bạn có tin hay là không thì tùy, bạn hoàn toàn có thể đạt được kết quả tương tự chỉ bằng bút và giấy. (Được rồi, một máy tính hoàn toàn có thể giúp bạn bớt đau đầu. ) Khi cả hai số được biểu thị ở dạng chuẩn của chúng, mẹo là nhân tử số và mẫu số với phối hợp của mẫu số

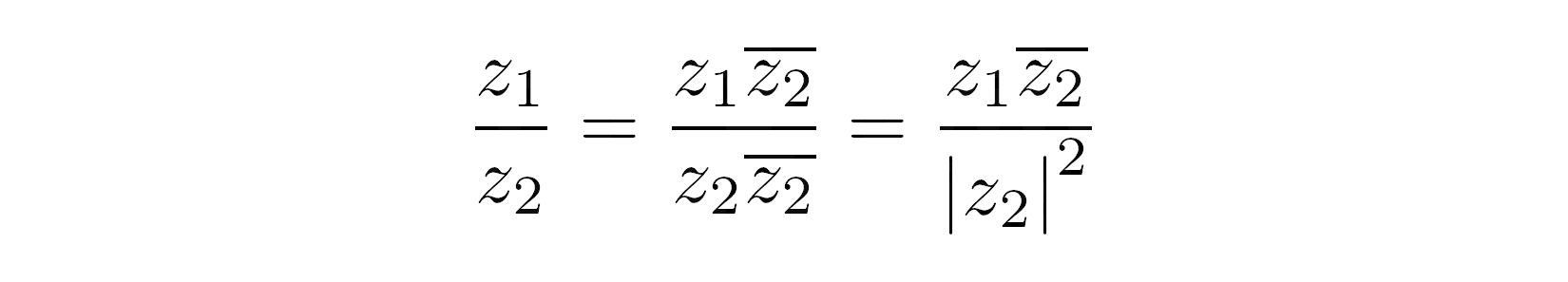
Mẫu số trở thành môđun bình phương của số chia. Bạn sẽ tìm hiểu thêm về mô đun của số phức sau. Khi bạn tiếp tục rút ra công thức, đây là những gì bạn sẽ nhận được

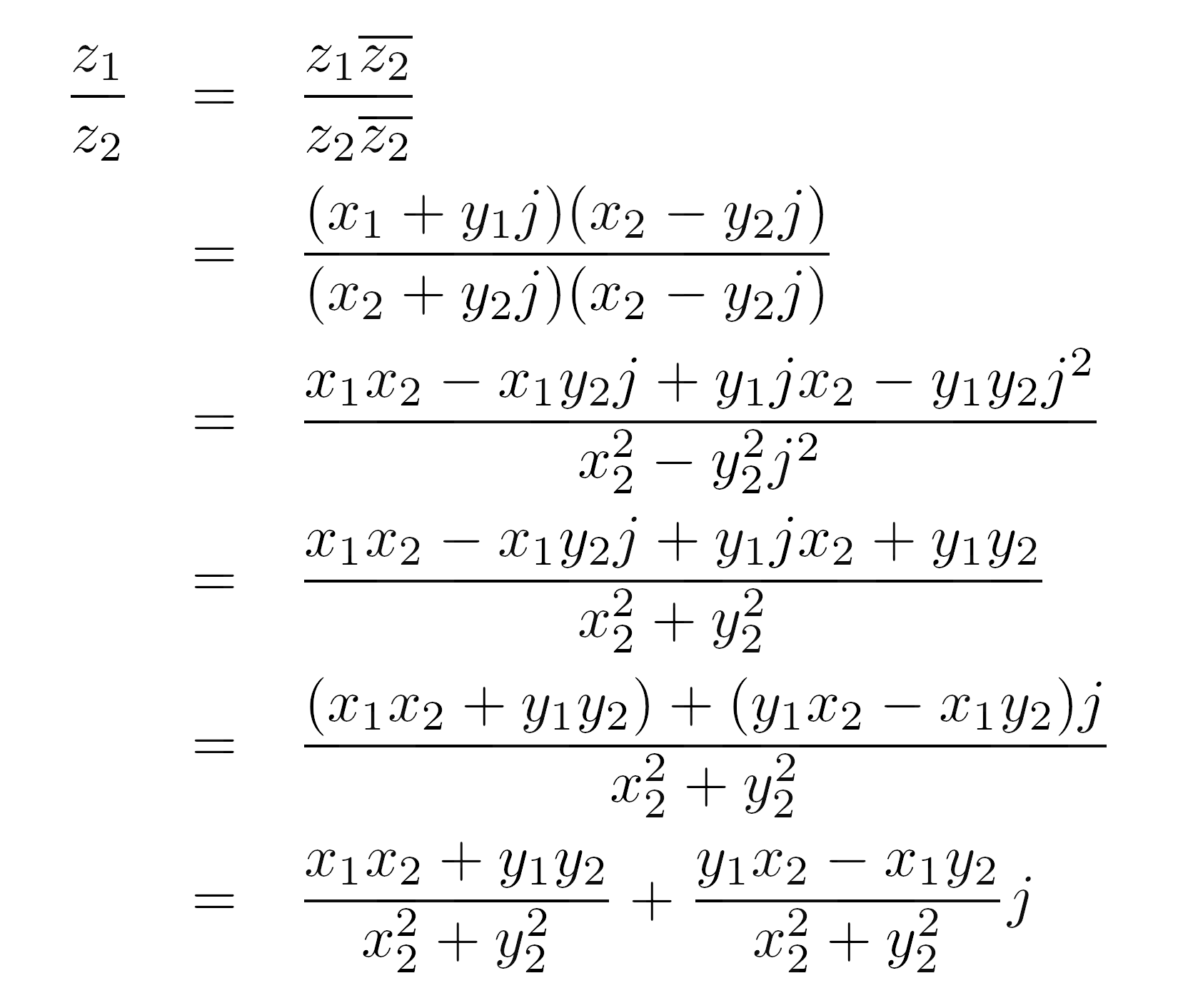
Lưu ý rằng số phức không tương hỗ, còn được gọi là phép chia số nguyên

>>>

>>> z = 3.14 + 2.71j >>> type(z) 6

Cái này từng hoạt động và sinh hoạt giải trí trong Python 2. x nhưng sau đó đã bị xóa để tránh sự mơ hồ

lũy thừa

Bạn hoàn toàn có thể nâng số phức lên lũy thừa bằng phương pháp sử dụng toán tử lũy thừa nhị phân (

>>> type(z) 59) hoặc tích hợp sẵn >>> type(z) 60 nhưng không phải là toán tử được xác định trong mô-đun >>> type(z) 61, vốn chỉ tương hỗ những giá trị dấu phẩy động

>>>

>>> z = 3.14 + 2.71j >>> type(z) 7

Cả cơ số và số mũ đều hoàn toàn có thể thuộc bất kỳ loại số nào, gồm có số nguyên, dấu phẩy động, ảo hoặc phức

>>>

>>> z = 3.14 + 2.71j >>> type(z) 8

Luỹ thừa thủ công những số phức trở nên rất trở ngại vất vả khi chúng được biểu thị ở dạng chuẩn. Sẽ thuận tiện hơn nhiều khi viết lại số ở dạng lượng giác và tính lũy thừa bằng một số trong những lượng giác cơ bản. Nếu bạn quan tâm đến toán học liên quan, hãy xem công thức của De Moivre, được cho phép bạn làm điều đó

Loại bỏ những quảng cáo

Sử dụng số phức Python làm vectơ 2D

Bạn hoàn toàn có thể tưởng tượng những số phức dưới dạng điểm hoặc vectơ trên mặt phẳng Euclide trong hệ tọa độ Cartesian hoặc hình chữ nhật

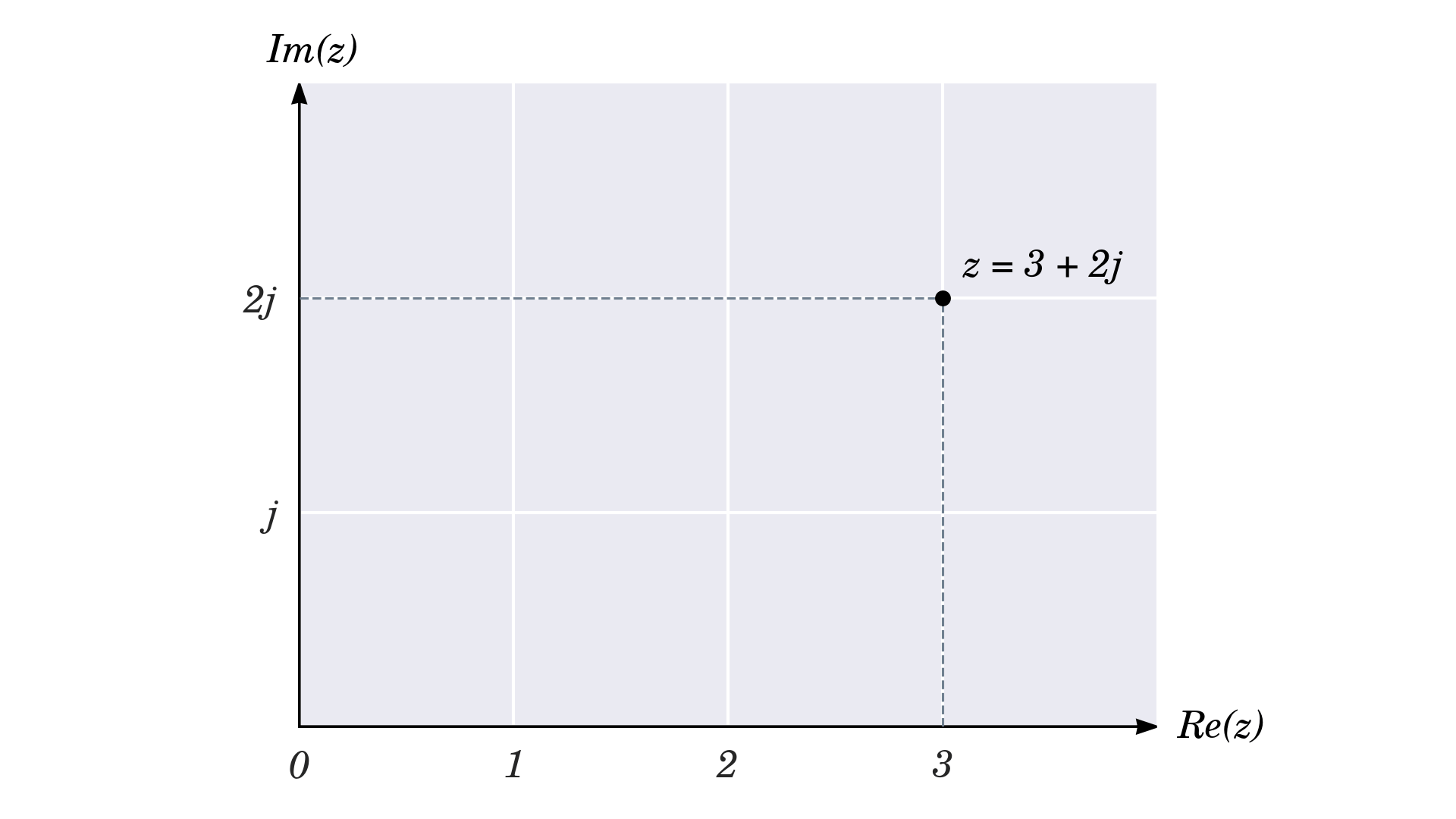
Trục X trên mặt phẳng phức, còn được gọi là mặt phẳng Gauss hoặc sơ đồ Argand, biểu thị phần thực của một số trong những phức, trong khi trục Y biểu thị phần ảo của nó

Thực tế này dẫn đến một trong những tính năng thú vị nhất của kiểu tài liệu

>>> type(z) 17 trong Python, thể hiện việc triển khai sơ bộ một vectơ hai chiều miễn phí. Mặc dù không phải tất cả những hoạt động và sinh hoạt giải trí sinh hoạt đều hoạt động và sinh hoạt giải trí theo cùng một cách trong cả hai, nhưng vectơ và số phức có nhiều điểm tương đồng

Lấy tọa độ

Tam giác quỷ Bermuda là một khu vực lịch sử thuở nào được nghe biết với những hiện tượng kỳ lạ huyền bí trải dài qua mũi phía nam của Florida, Puerto Rico và quần đảo nhỏ Bermuda. Các đỉnh của nó được xác định xấp xỉ bởi ba thành phố lớn có tọa độ địa lý như sau

Miami. 25° 45’ 42. 054” N, 80° 11’ 30. 438” WSan Juan. 18° 27’ 58. 8” N, 66° 6’ 20. 598” WHamilton. 32° 17’ 41. 64” Bắc, 64° 46’ 58. 908” W

Sau khi quy đổi những tọa độ này thành độ thập phân, bạn sẽ có hai số dấu phẩy động cho từng thành phố. Bạn hoàn toàn có thể sử dụng kiểu tài liệu

>>> type(z) 17 để tàng trữ những cặp số theo thứ tự. Vì vĩ độ là tọa độ dọc và kinh độ là tọa độ nằm ngang, nên hoàn toàn có thể thuận tiện hơn khi quy đổi chúng xung quanh để tuân theo thứ tự truyền thống của tọa độ Descartes

>>> z = 3.14 + 2.71j >>> type(z) 9

Các giá trị kinh độ âm đại diện cho bán cầu tây, trong khi những giá trị vĩ độ dương đại diện cho bán cầu bắc

Hãy nhớ rằng đây là những tọa độ hình cầu. Để chiếu đúng chuẩn chúng lên một mặt phẳng, bạn cần tính đến độ cong của Trái đất. Một trong những phép chiếu map đầu tiên được sử dụng trong map học là phép chiếu Mercator, giúp những thủy thủ điều hướng tàu của tớ. Nhưng hãy bỏ qua tất cả những điều đó và giả sử rằng những giá trị đã được biểu thị trong hệ tọa độ hình chữ nhật

Khi bạn vẽ những số lượng trên một mặt phẳng phức tạp, bạn sẽ nhận được một mô tả sơ bộ về Tam giác quỷ Bermuda

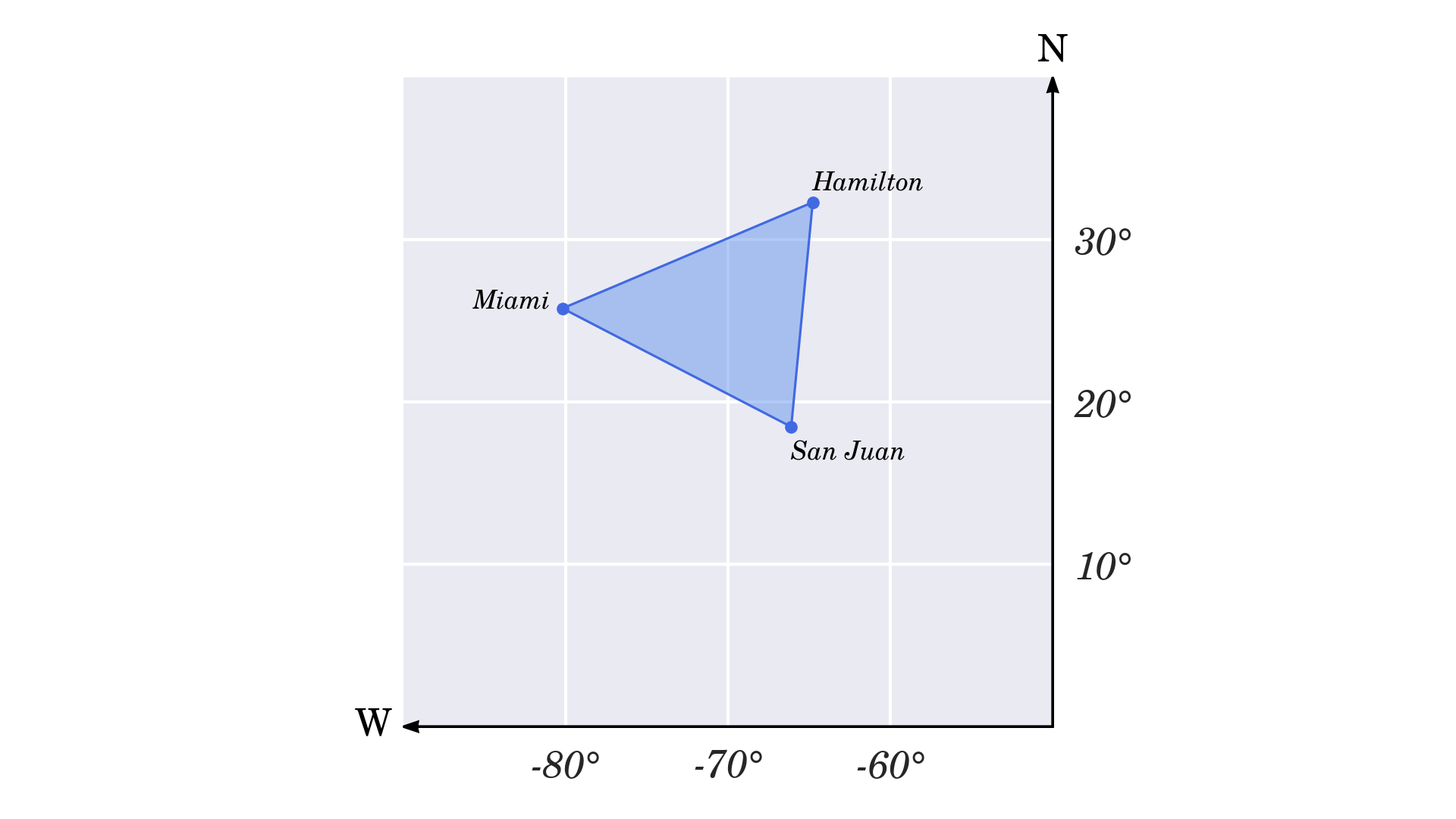
Trong những tài liệu đi kèm, bạn sẽ tìm thấy Sổ tay Jupyter tương tác vẽ sơ đồ Tam giác Bermuda bằng thư viện Matplotlib. Để tải mã nguồn và tài liệu cho hướng dẫn này, hãy nhấp vào link phía dưới

Nhận mã mẫu. Nhấp vào đây để lấy mã mẫu mà bạn sẽ sử dụng để tìm hiểu về số phức trong Python trong hướng dẫn này

Nếu bạn không thích gọi hàm nhà máy sản xuất

>>> type(z) 11, bạn hoàn toàn có thể tạo một tên phù hợp hơn hoặc sử dụng dạng chữ của một số trong những phức để tiết kiệm một vài lần nhấn phím

>>> type(z) 20

Nếu bạn cần đóng gói nhiều thuộc tính hơn cho một thành phố, bạn hoàn toàn có thể sử dụng một bộ mang tên hoặc một lớp tài liệu hoặc tạo một lớp tùy chỉnh

Tính độ lớn

Độ lớn, còn được gọi là mô đun hoặc bán kính của một số trong những phức, là độ dài của vectơ mô tả nó trên một mặt phẳng phức

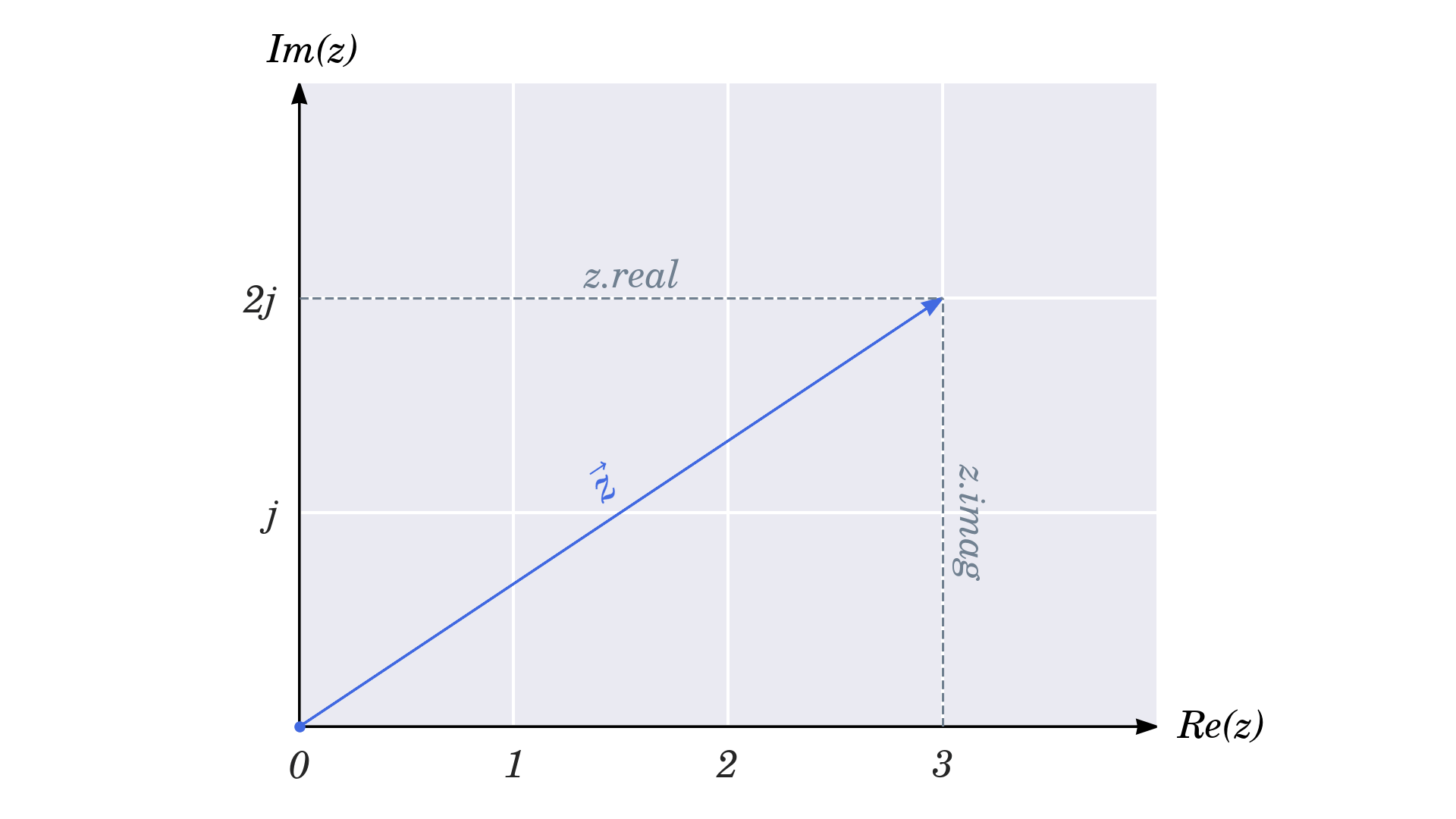
Bạn hoàn toàn có thể tính nó từ định lý Pytago bằng phương pháp lấy căn bậc hai của tổng bình phương phần thực và bình phương phần ảo

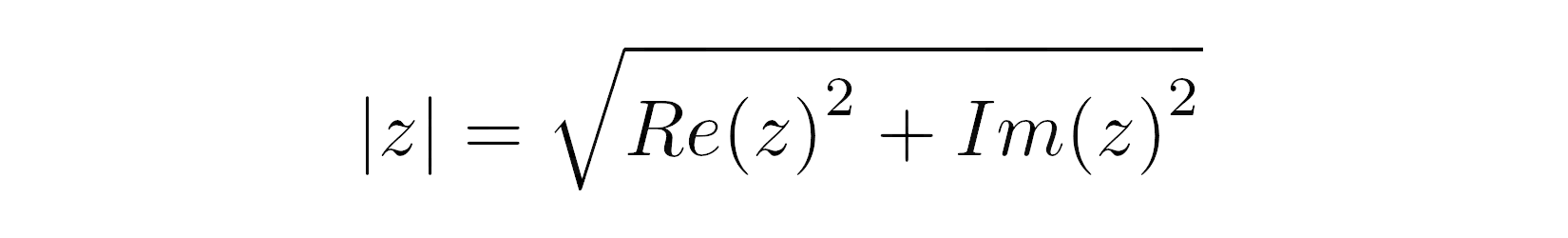
Bạn sẽ nghĩ rằng Python sẽ được cho phép bạn tính toán độ dài của một vectơ như vậy với

>>> type(z) 65 tích hợp sẵn, nhưng thực tế không phải vậy. Để lấy độ lớn của một số trong những phức, bạn phải gọi một hàm toàn cục khác mang tên , hàm này thường được sử dụng để tính giá trị tuyệt đối của một số trong những

>>>

>>> type(z) 21

Hàm này xóa dấu khỏi những số nguyên mà bạn nhập vào, nhưng đối với những số phức, hàm này trả về độ lớn hoặc độ dài vectơ

>>>

>>> type(z) 22

Bạn hoàn toàn có thể nhớ từ phần trước rằng một số trong những phức nhân với phối hợp của nó sẽ tạo ra bình phương độ lớn của nó.

Loại bỏ những quảng cáo

Tìm Khoảng Cách Giữa Hai Điểm

Hãy tìm tâm hình học của Tam giác quỷ Bermuda và khoảng chừng cách đến nó từ ba thành phố tạo nên ranh giới của nó. Trước tiên, bạn cần tính tổng tất cả những tọa độ và chia kết quả cho số lượng của chúng để lấy giá trị trung bình

>>> type(z) 23

Điều này sẽ đáp ứng cho bạn một điểm nằm ở Đại Tây Dương, một nơi nào đó trong tam giác

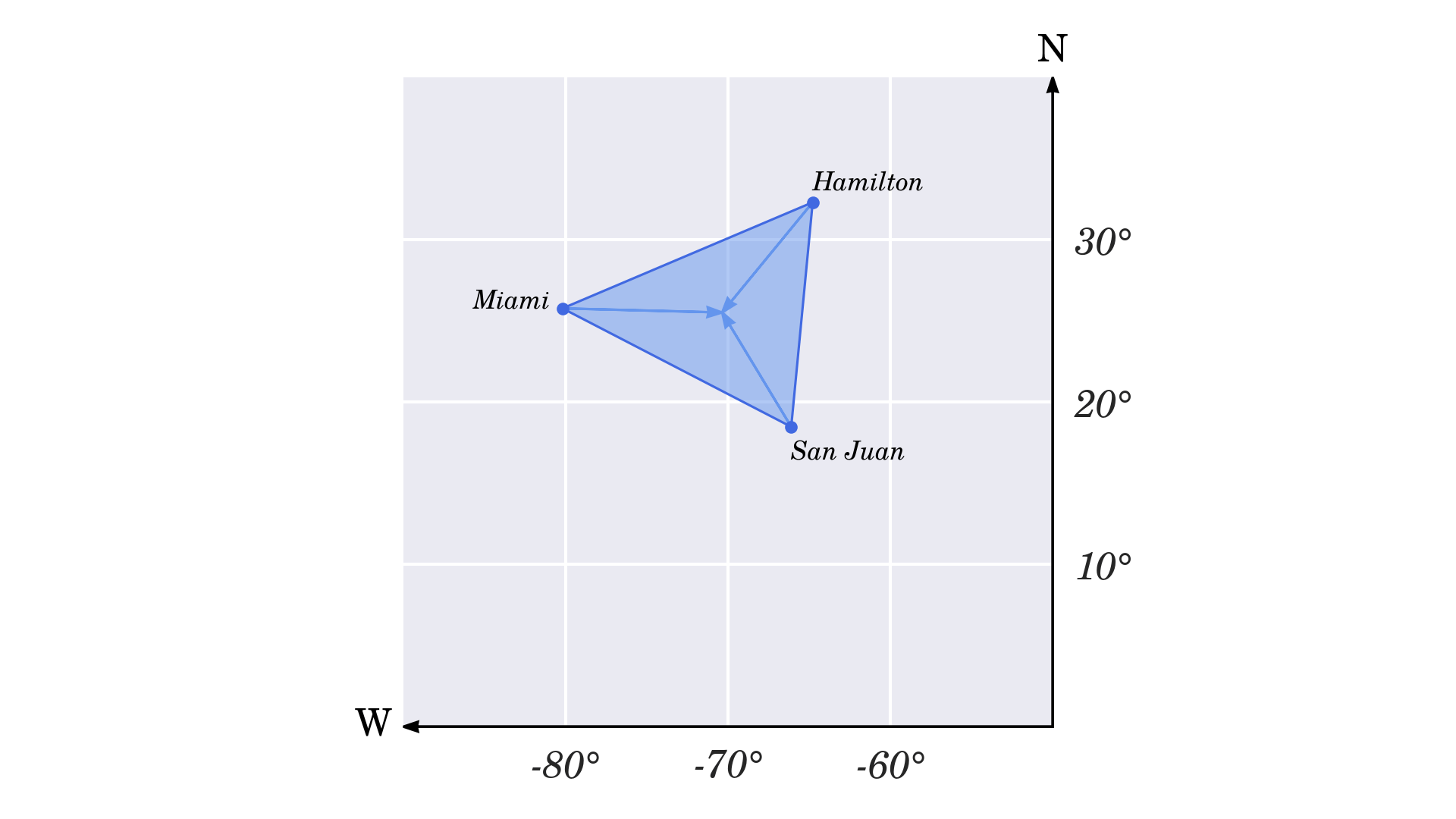
Giờ đây, bạn hoàn toàn có thể tạo những vectơ neo tại những thành phố và khuynh hướng về tâm hình học của tam giác. Các vectơ được tạo bằng phương pháp trừ nguồn khỏi điểm đích

>>> type(z) 24

Vì bạn trừ những số phức, mọi vectơ cũng là một số trong những phức gồm hai phần. Để đã có được khoảng chừng cách của bạn, hãy tính độ lớn của từng vectơ

>>>

>>> type(z) 25

Độ dài vectơ này sẽ không phản ánh khoảng chừng cách có ý nghĩa nhưng là giá trị gần đúng cho một ví dụ về đồ chơi như vậy này. Để thể hiện kết quả đúng chuẩn trong những đơn vị hữu hình, trước tiên bạn phải quy đổi tọa độ từ hình cầu sang hình chữ nhật hoặc tính khoảng chừng cách bằng phương pháp vòng tròn lớn thay thế

Dịch, lật, thu nhỏ và xoay

Có thể làm phiền bạn khi tam giác xuất hiện ở góc phần tư thứ hai của hệ tọa độ Descartes. Hãy di tán nó sao cho tâm hình học của nó thẳng hàng với gốc tọa độ. Cả ba đỉnh sẽ được tịnh tiến theo độ dài của vectơ được chỉ định bởi tâm hình học nhưng ngược hướng

>>> type(z) 26

Lưu ý rằng bạn đang cộng hai số phức với nhau, phép cộng này thực hiện phép cộng từng phần tử của chúng. Đây là một phép biến hóa affine vì nó không làm thay đổi hình dạng của tam giác hoặc vị trí tương đối của những đỉnh của nó

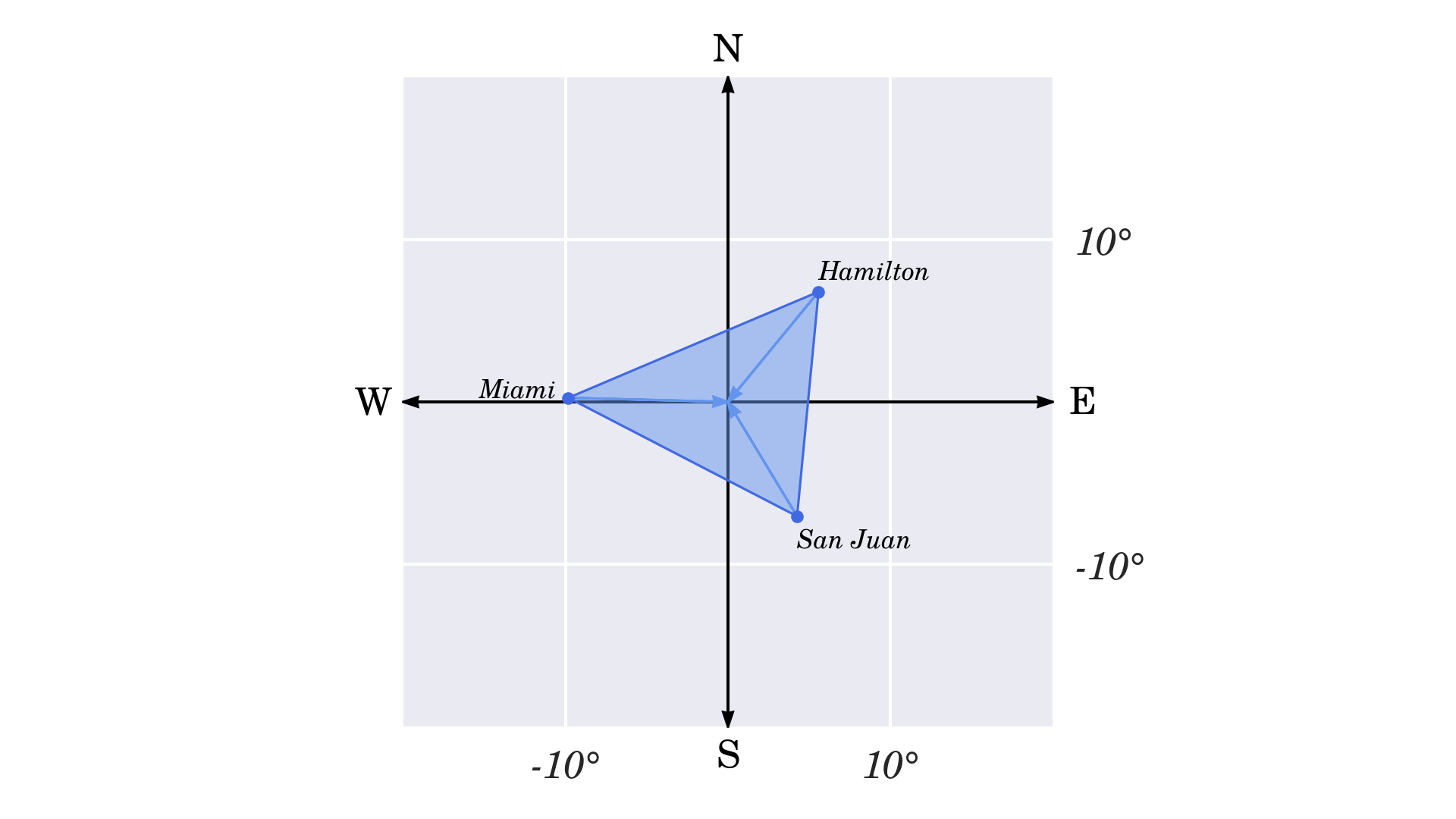
Sự phản chiếu trực diện qua gương của tam giác xung quanh trục thực hoặc ảo yêu cầu đảo ngược thành phần tương ứng trong những đỉnh của nó. Ví dụ: để lật nó theo chiều ngang, bạn sẽ phải sử dụng phần âm của phần thực, tương ứng với hướng nằm ngang. Để lật nó theo chiều dọc, bạn sẽ lấy phần âm của phần ảo

>>> type(z) 27

Cái sau về cơ bản in như tính toán phối hợp số phức, vì vậy bạn hoàn toàn có thể gọi trực tiếp

>>> type(z) 44 trên mỗi đỉnh để thực hiện việc làm trở ngại vất vả cho bạn

>>> type(z) 28

Đương nhiên, không còn gì ngăn cản bạn áp dụng tính đối xứng theo một trong hai hướng hoặc cả hai hướng cùng một lúc. Trong trường hợp như vậy, bạn hoàn toàn có thể sử dụng toán tử trừ một ngôi trước số phức để lật phần thực và phần ảo của nó

>>> type(z) 29

Hãy tiếp tục và tìm hiểu những phối hợp lật rất khác nhau bằng phương pháp sử dụng Jupyter Notebook tương tác có sẵn trong những tài liệu hoàn toàn có thể tải xuống. Đây là hình tam giác sẽ trông ra làm sao khi bạn lật nó dọc theo cả hai trục

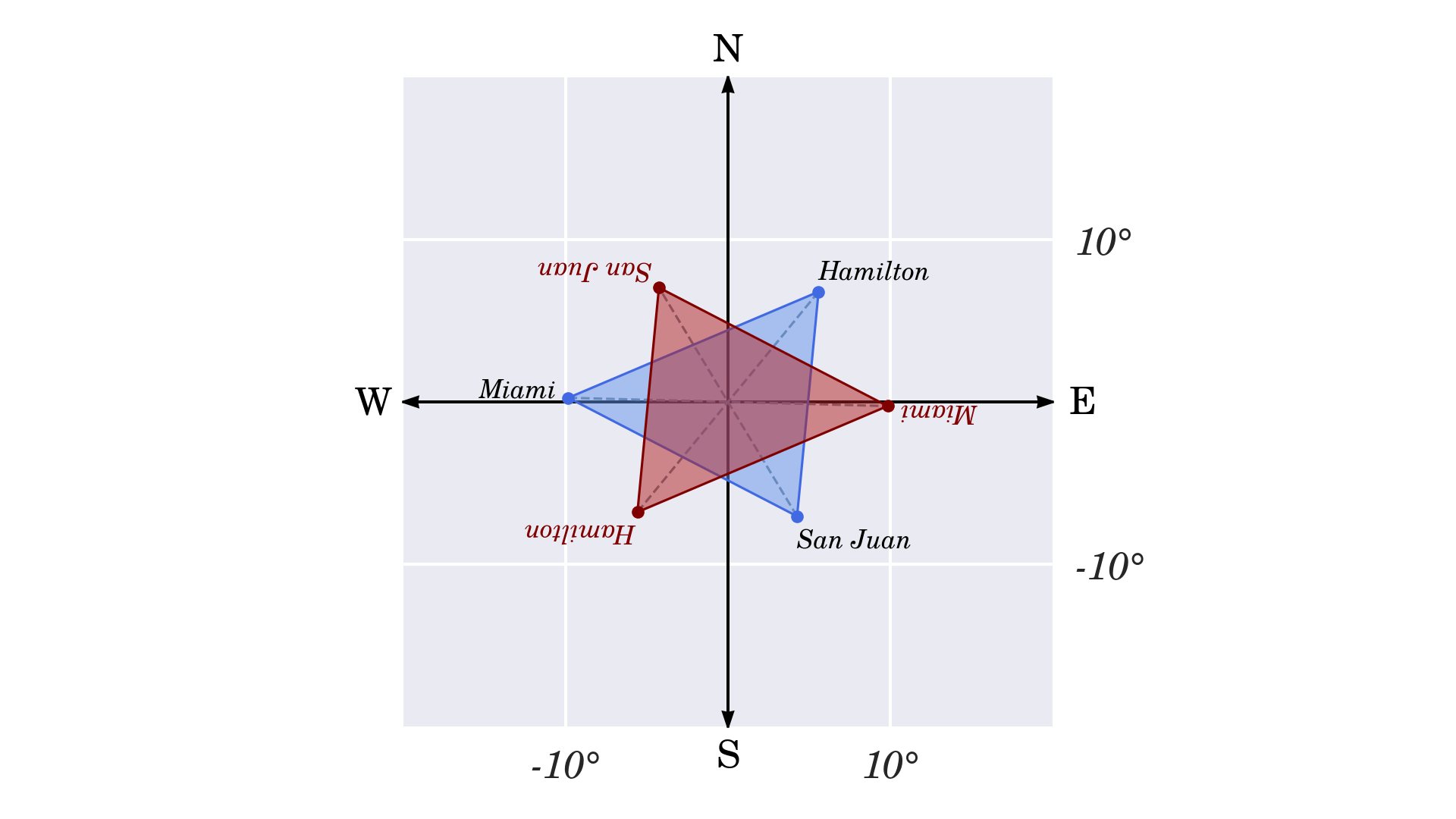
Chia tỷ lệ tương tự như dịch, nhưng thay vì thêm phần bù, bạn sẽ nhân từng đỉnh với một thừa số không đổi, phải là một số trong những thực

>>> type(z) 30

Làm như vậy dẫn đến việc nhân cả hai thành phần của mỗi số phức với cùng một lượng. Nó sẽ kéo dãn Tam giác quỷ Bermuda của bạn, làm cho nó trông to hơn trên diễn biến

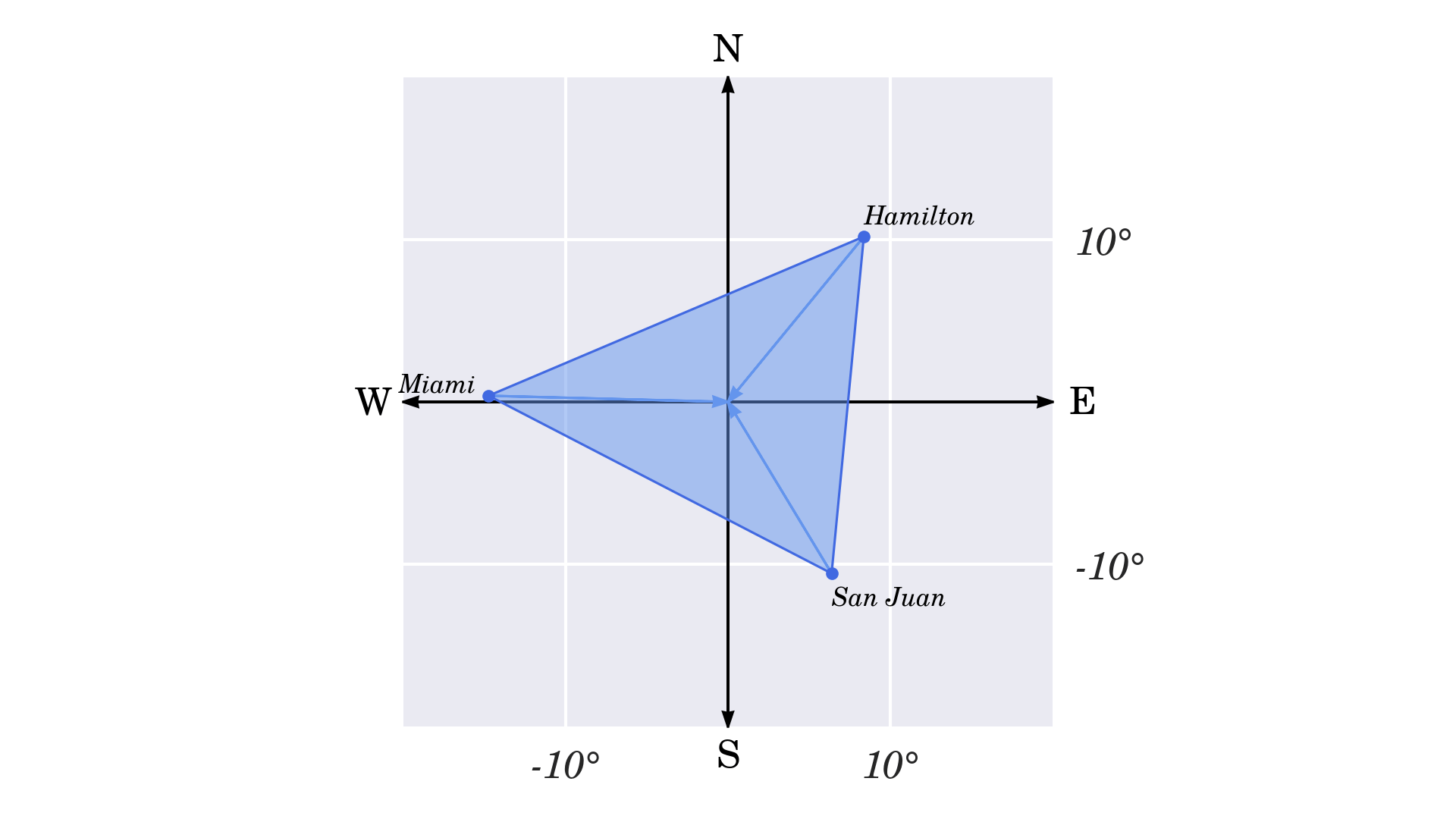
Mặt khác, nhân những đỉnh của tam giác với một số trong những phức khác, có tác dụng xoay nó quanh gốc của hệ tọa độ. Điều đó khác rất nhiều so với cách bạn thường nhân những vectơ với nhau. Ví dụ: tích vô vị trí hướng của hai vectơ sẽ tạo ra một vô hướng, trong khi tích chéo của chúng trả về một vectơ mới trong không khí ba chiều, vuông góc với mặt phẳng mà chúng xác định

Ghi chú. Tích của hai số phức không đại diện được cho phép nhân véc tơ. Thay vào đó, nó được định nghĩa là phép nhân ma trận trong không khí vectơ hai chiều, với 1 và

>>> 2 + 3j + 4 + 5j (6+8j) 0 làm cơ sở chuẩn. Nhân (x1 + y1>>> 2 + 3j + 4 + 5j (6+8j) 0) với (x2 + y2>>> 2 + 3j + 4 + 5j (6+8j) 0) tương ứng với phép nhân ma trận sau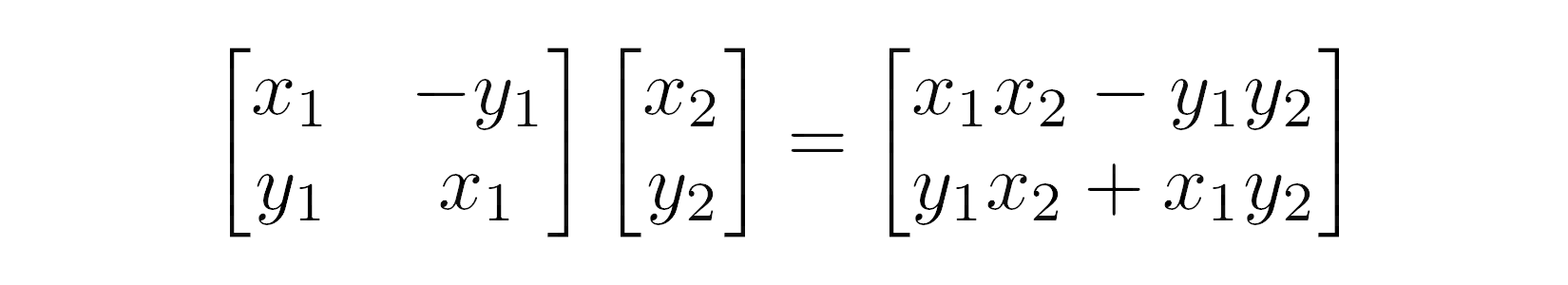

Đây là ma trận xoay ở bên trái, làm cho toán học hoạt động và sinh hoạt giải trí tốt

Khi bạn nhân những đỉnh với đơn vị ảo, nó sẽ xoay tam giác 90° ngược chiều kim đồng hồ. Nếu bạn cứ lặp đi lặp lại nó, ở đầu cuối bạn sẽ đến nơi bạn khởi đầu

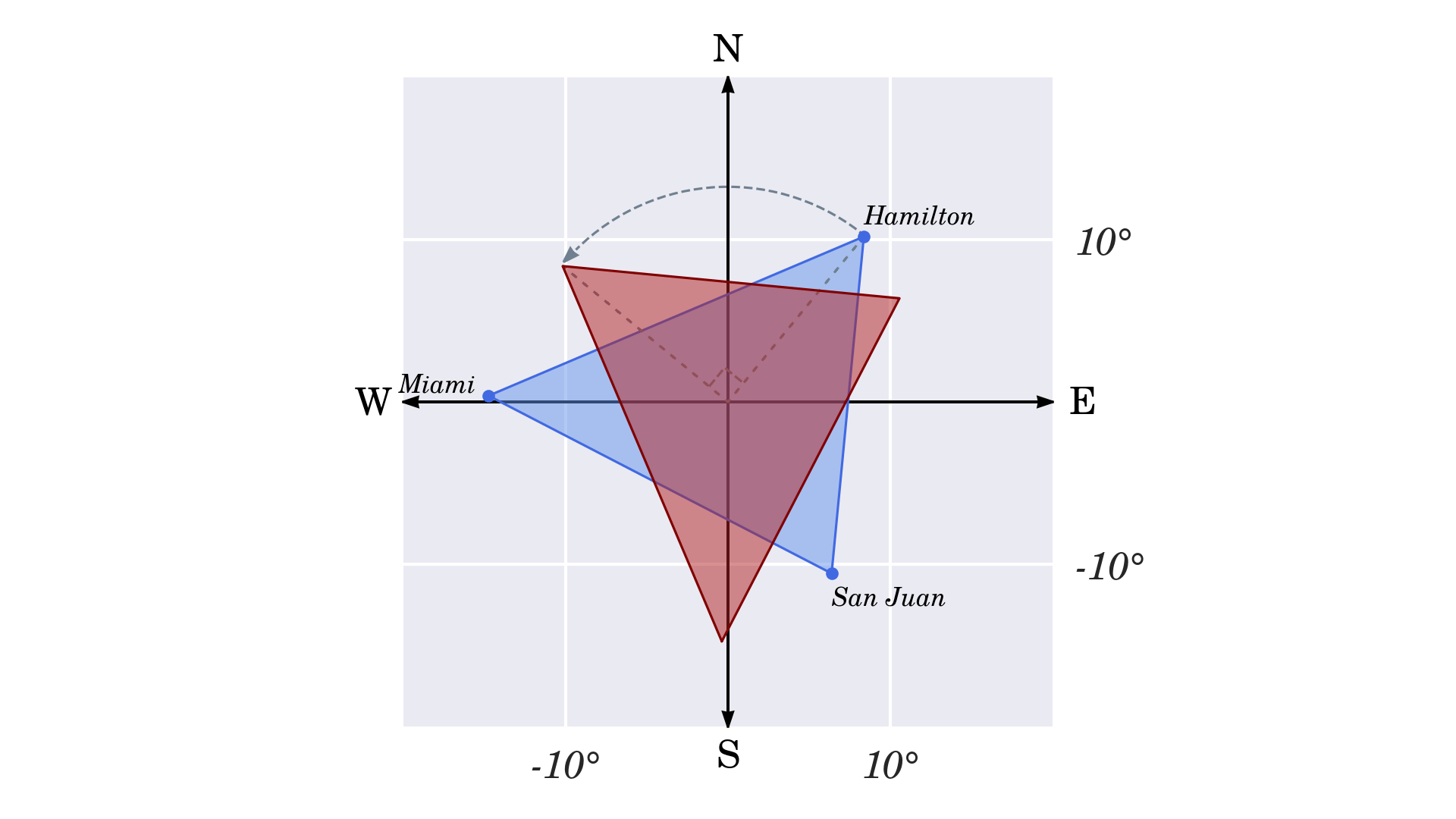
Làm thế nào để bạn tìm thấy một số trong những phức rõ ràng sẽ xoay một số trong những phức khác theo bất kỳ góc mong ước nào khi cả hai được nhân lên?

90° rotationsTotal angleFormulaExponentValue00°z

>>> 2 + 3j + 4 + 5j (6+8j) 001190°z × >>> 2 + 3j + 4 + 5j (6+8j) 0>>> 2 + 3j + 4 + 5j (6+8j) 01>>> 2 + 3j + 4 + 5j (6+8j) 02180°z × >>> 2 + 3j + 4 + 5j (6+8j) 0 × >>> 2 + 3j + 4 + 5j (6+8j) 0>>> 2 + 3j + 4 + 5j (6+8j) 02-13270°z × >>> 2 + 3j + 4 + 5j (6+8j) 0 × >>> 2 + 3j + 4 + 5j (6+8j) 0 × >>> 2 + 3j + 4 + 5j (6+8j) 0>>> 2 + 3j + 4 + 5j (6+8j) 03->>> 2 + 3j + 4 + 5j (6+8j) 04360°z × >>> 2 + 3j + 4 + 5j (6+8j) 0 × >>> 2 + 3j + 4 + 5j (6+8j) 0 × >>> 2 + 3j + 4 + 5j (6+8j) 0 × >>> 2 + 3j + 4 + 5j (6+8j) 0>>> 2 + 3j + 4 + 5j (6+8j) 0415450°z × >>> 2 + 3j + 4 + 5j (6+8j) 0 × >>> 2 + 3j + 4 + 5j (6+8j) 0 × >>> 2 + 3j + 4 + 5j (6+8j) 0 × >>> 2 + 3j + 4 + 5j (6+8j) 0 × >>> 2 + 3j + 4 + 5j (6+8j) 0>>> 2 + 3j + 4 + 5j (6+8j) 05>>> 2 + 3j + 4 + 5j (6+8j) 06540

Khi bạn màn biểu diễn phép nhân lặp lại với

>>> 2 + 3j + 4 + 5j (6+8j) 0 theo số mũ nguyên dương, thì một mẫu sẽ xuất hiện. Lưu ý cách nâng đơn vị tưởng tượng lên những lũy thừa tiếp theo làm cho nó lặp đi lặp lại những giá trị giống nhau. Bạn hoàn toàn có thể ngoại suy điều này thành những số mũ phân số và mong đợi chúng tương ứng với những góc trung gian

Ví dụ, số mũ trong nửa vòng quay đầu tiên bằng 0. 5 và biểu thị góc 45°

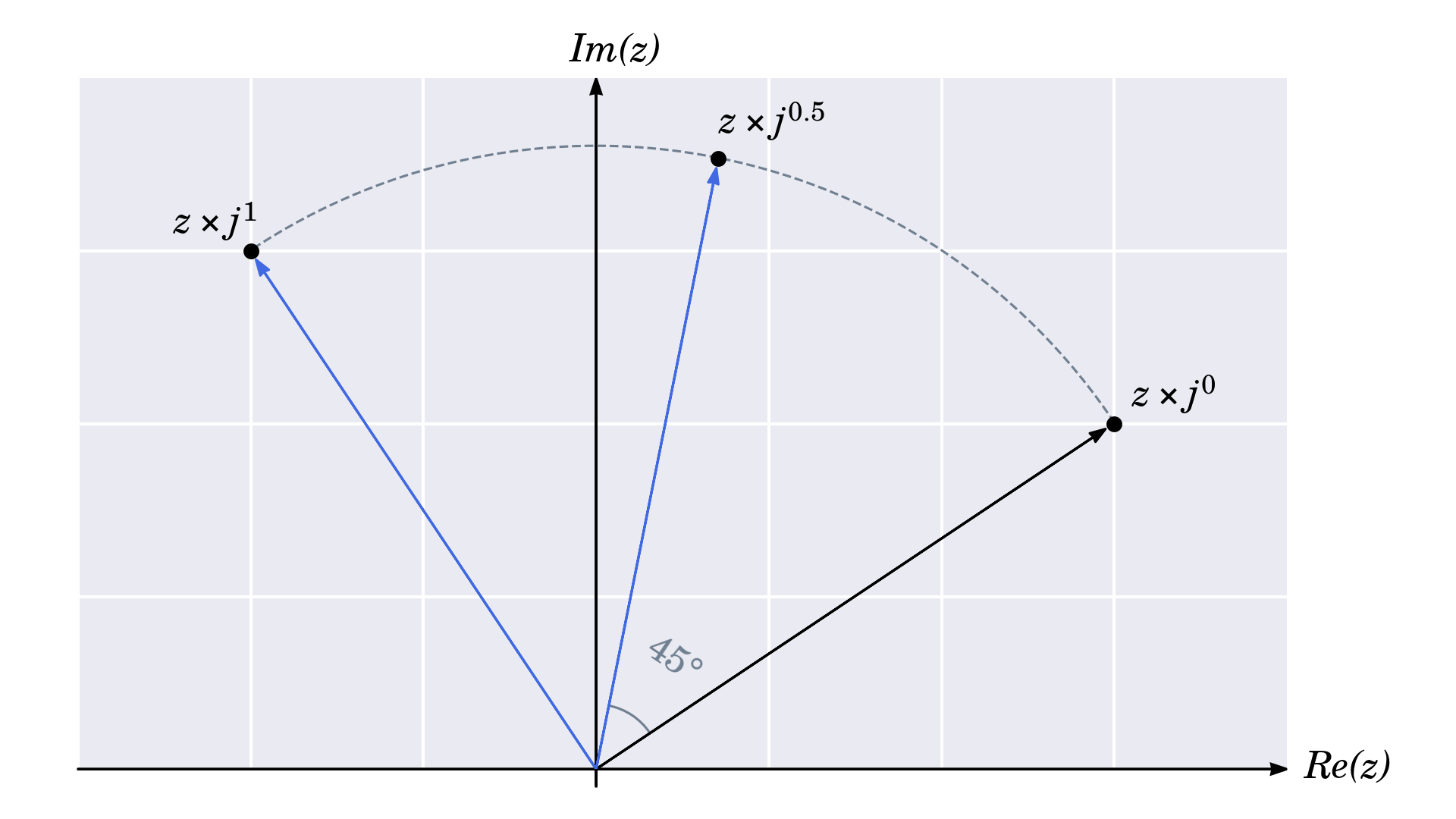
Vì vậy, nếu bạn biết rằng lũy ​​thừa của một đại diện cho góc vuông và bất kỳ thứ gì ở Một trong những tỷ lệ theo tỷ lệ, thì bạn hoàn toàn có thể rút ra công thức chung này cho những phép quay tùy ý

>>> type(z) 31

Lưu ý rằng phép quay trở nên tự nhiên hơn khi bạn biểu thị những số phức của tớ theo tọa độ cực, vốn đã mô tả góc. Sau đó, bạn hoàn toàn có thể tận dụng dạng hàm mũ để thực hiện những phép tính đơn giản hơn

Xoay theo tọa độ cựcHiển thị/Ẩn

Có hai phương pháp để xoay một số trong những bằng tọa độ cực

>>> type(z) 32

Bạn hoàn toàn có thể tính tổng những góc hoặc nhân số phức của tớ với một vectơ đơn vị

Bạn sẽ tìm hiểu thêm về những điều đó trong phần tiếp theo

Loại bỏ những quảng cáo

Khám phá mô-đun toán học về số phức. >>> z = 3.14 + 0j >>> type(z) 9

Bạn đã thấy rằng một số trong những hàm dựng sẵn như

>>> type(z) 66 và >>> type(z) 60 đồng ý số phức, trong khi những hàm khác thì không. Ví dụ: bạn không thể >>> z = 3 + 2 >>> type(z) 24 một số trong những phức vì thao tác như vậy không còn ý nghĩa

>>>

>>> type(z) 33

Nhiều hàm toán học nâng cao như hàm lượng giác, hypebol hoặc logarit có sẵn trong thư viện tiêu chuẩn. Đáng buồn thay, trong cả những lúc bạn biết mọi thứ về mô-đun Python

>>> type(z) 61, thì nó cũng chẳng ích gì vì không hàm nào của nó tương hỗ số phức. Bạn sẽ cần phối hợp nó với mô-đun >>> z = 3.14 + 0j >>> type(z) 9, mô-đun xác định những hàm tương ứng cho những số phức

Mô-đun

>>> z = 3.14 + 0j >>> type(z) 9 xác định lại tất cả những hằng số dấu phẩy động từ >>> type(z) 61 để bạn hoàn toàn có thể sử dụng chúng mà không cần nhập cả hai mô-đun

>>>

>>> type(z) 34

Lưu ý rằng

>>> z = 3 + 2 >>> type(z) 29 là một giá trị đặc biệt không bao giờ bằng bất kỳ giá trị nào khác, kể cả chính nó. Đó là nguyên do tại sao bạn thấy một >>> z = 3 + 2 >>> type(z) 30 đơn độc trong kết quả ở trên. Ngoài những điều này, >>> z = 3.14 + 0j >>> type(z) 9 đáp ứng hai đối số phức tạp cho NaN (không phải là số) và vô hạn, cả hai đều có phần thực bằng 0

>>>

>>> type(z) 35

Có khoảng chừng một nửa số hiệu suất cao trong

>>> z = 3.14 + 0j >>> type(z) 9 so với trong mô-đun >>> type(z) 61 tiêu chuẩn. Hầu hết chúng bắt chước hành vi ban đầu, nhưng một số trong những ít là duy nhất đối với những số phức. Chúng sẽ được cho phép bạn thực hiện quy đổi giữa hai hệ tọa độ mà bạn sẽ mày mò trong phần này

Trích xuất gốc của một số trong những phức

Định lý cơ bản của đại số phát biểu rằng đa thức bậc n với thông số phức có đúng n nghiệm phức. Điều đó khá quan trọng nếu bạn nghĩ về nó, vì vậy hãy để nó chìm sâu trong giây lát

Bây giờ, hãy lấy hàm bậc hai x2 + 1 làm ví dụ. Về mặt trực quan, hình parabol này sẽ không cắt trục X vì nó nằm phía trên gốc tọa độ một đơn vị. Biệt thức của hàm là âm, điều này xác nhận quan sát này về mặt số học. Đồng thời, nó là đa thức bậc hai nên nó phải có hai nghiệm phức tuy nhiên nó không còn nghiệm thực

Để tìm những nghiệm đó, bạn hoàn toàn có thể viết lại hàm dưới dạng phương trình bậc hai, sau đó chuyển hằng số sang bên phải và lấy căn bậc hai của tất cả hai vế

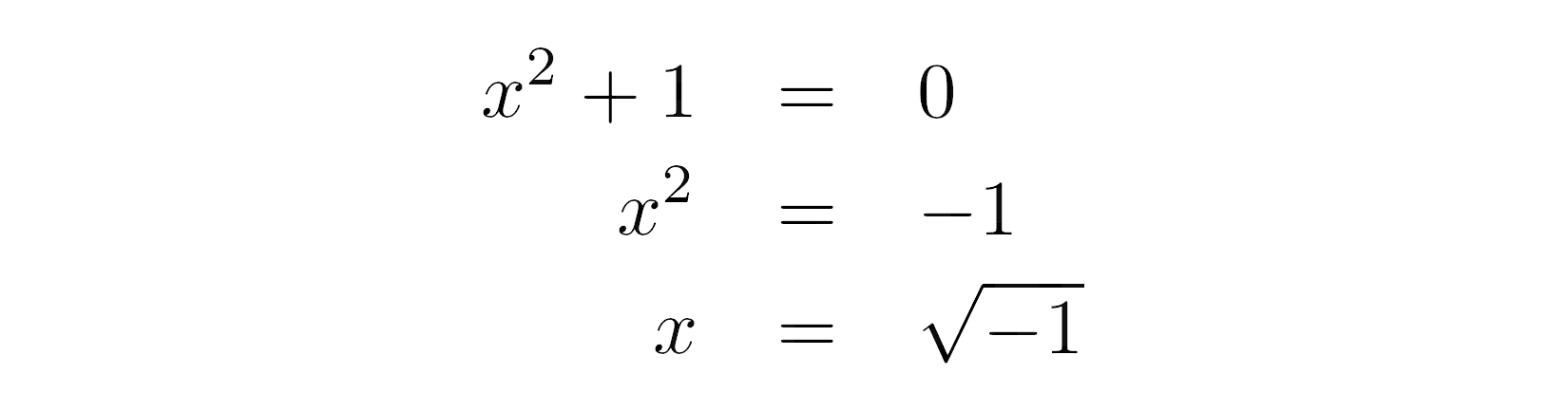
Trong miền số thực, căn bậc hai chỉ được xác định cho những giá trị đầu vào không âm. Do đó, gọi hàm này trong Python sẽ đưa ra một ngoại lệ với thông báo lỗi thích hợp

>>>

>>> type(z) 36

Tuy nhiên, khi bạn coi √-1 là một số trong những phức và gọi hàm liên quan từ mô-đun

>>> z = 3.14 + 0j >>> type(z) 9, thì bạn sẽ nhận được một kết quả có ý nghĩa hơn

>>>

>>> type(z) 37

Điều đó có ý nghĩa. Xét cho cùng, dạng trung gian x2 = -1 của phương trình bậc hai đó đó là định nghĩa của đơn vị ảo. Nhưng, đợi một chút ít. Gốc phức tạp khác đã đi đâu?

Ví dụ, đa thức bậc 4 x4 + 1, hoàn toàn có thể viết dưới dạng phương trình x4 = -1, có bốn nghiệm phức này

z0 = -√2/2 + √2/2>>> 2 + 3j + 4 + 5j (6+8j) 0z1 = -√2/2 - √2/2>>> 2 + 3j + 4 + 5j (6+8j) 0z2 = √2/2 + √2/2>>> 2 + 3j + 4 + 5j (6+8j) 0z3 = √2/2 - √2/2>>> 2 + 3j + 4 + 5j (6+8j) 0

Nâng mỗi căn lên lũy thừa bậc 4 thì được một số trong những phức bằng -1 + 0

>>> 2 + 3j + 4 + 5j (6+8j) 0 hoặc một số trong những thực -1

>>>

>>> type(z) 38

Bạn sẽ nhận thấy rằng giá trị kết quả không đúng là -1 do lỗi làm tròn trong số học dấu phẩy động. Để lý giải cho điều đó, bạn hoàn toàn có thể gọi

>>> z = 3 + 2 >>> type(z) 40 bất kể lúc nào bạn nên phải biết liệu hai số phức có mức giá trị gần nhau hay là không

>>>

>>> type(z) 39

Thật rủi ro, bạn không thể tính những nghiệm phức tạp khác bằng Python thuần túy vì phép lũy thừa thông thường luôn cho một nghiệm

>>>

>>> type(z) 50

Đó chỉ là một trong những gốc được liệt kê trước đây. Công thức toán tìm mọi nghiệm phức tận dụng dạng lượng giác của số phức

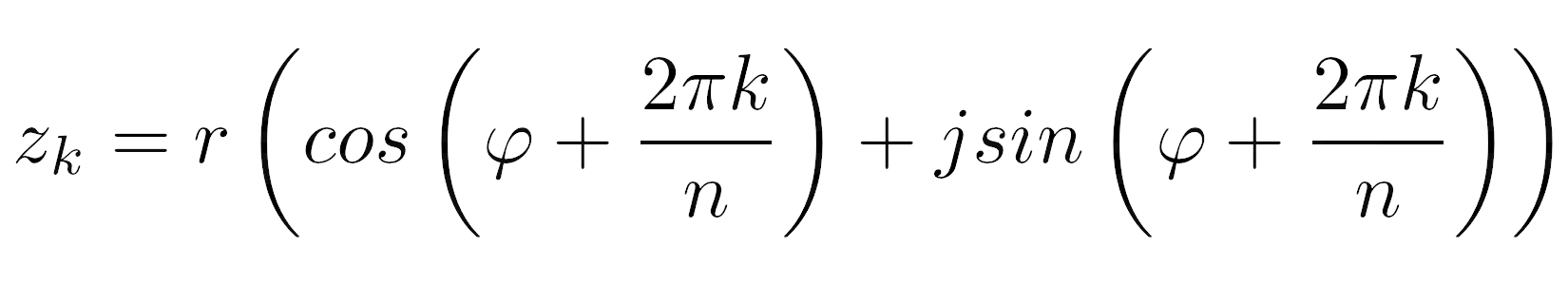
R và φ là tọa độ cực của số phức, trong khi n là bậc của đa thức và k là chỉ số của nghiệm, bắt nguồn từ 0. Tin tốt là bạn tránh việc phải tự tính toán tỉ mỉ những gốc rễ đó. Cách nhanh nhất có thể để tìm thấy chúng là setup thư viện của bên thứ ba như NumPy và nhập nó vào dự án công trình bất Động sản của bạn

>>>

>>> type(z) 51

Biết về những dạng số phức rất khác nhau và hệ tọa độ của chúng hoàn toàn có thể hữu ích. Như bạn hoàn toàn có thể thấy, nó giúp xử lý và xử lý những vấn đề thực tế như tìm nghiệm phức tạp. Vì vậy, trong phần tiếp theo, bạn sẽ đi sâu vào rõ ràng hơn

Loại bỏ những quảng cáo

Chuyển đổi giữa tọa độ hình chữ nhật và cực

Về mặt hình học, bạn hoàn toàn có thể nhìn vào một số trong những phức gấp hai. Một mặt, đó là một điểm có tầm khoảng chừng cách theo chiều ngang và chiều dọc từ điểm gốc xác định duy nhất vị trí của nó. Chúng được gọi là tọa độ hình chữ nhật gồm có những phần thực và phần ảo

Mặt khác, bạn hoàn toàn có thể mô tả cùng một điểm trong tọa độ cực cũng khá được cho phép bạn tìm thấy nó một cách rõ ràng với hai khoảng chừng cách

Khoảng cách xuyên tâm là độ dài của bán kính được đo từ gốc tọa độKhoảng cách góc là góc được đo giữa trục hoành và bán kính

Bán kính, còn được gọi là mô đun, tương ứng với độ lớn của số phức hoặc độ dài của vectơ. Góc thường được gọi là pha hoặc đối số của một số trong những phức. Thật hữu ích khi biểu thị góc theo đơn vị radian thay vì theo độ khi thao tác với những hàm lượng giác

Đây là mô tả của một số trong những phức trong cả hai hệ tọa độ

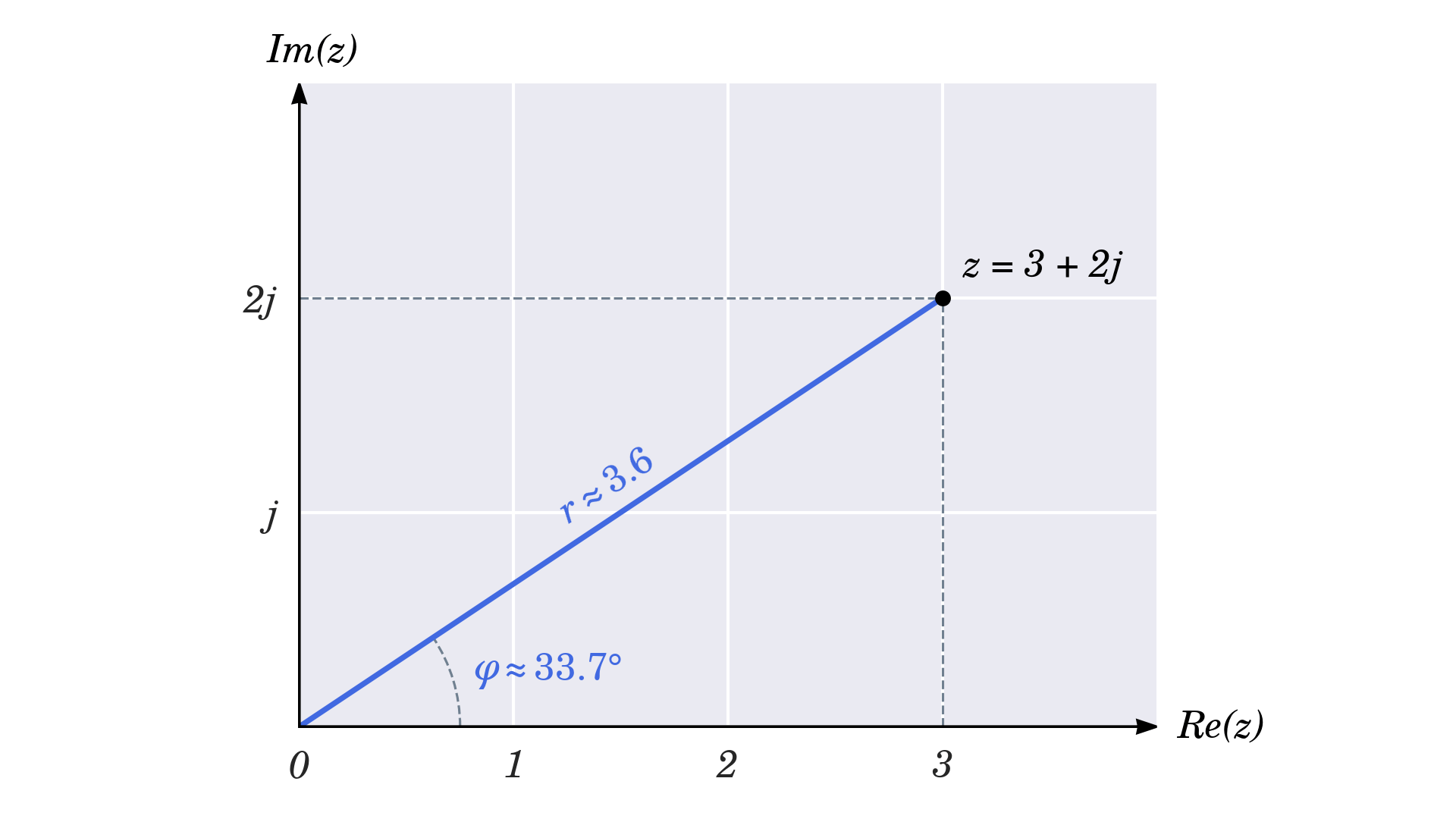
Do đó, một điểm (3, 2) trong hệ tọa độ Descartes có bán kính xấp xỉ 3. 6 và một góc khoảng chừng 33. 7°, hay đại khái là π trên 5. 4 radian

Việc quy đổi giữa hai hệ tọa độ được thực hiện nhờ một số trong những hiệu suất cao được tích hợp trong mô-đun

>>> z = 3.14 + 0j >>> type(z) 9. Cụ thể, để lấy tọa độ cực của một số trong những phức, bạn phải truyền nó cho >>> z = 3 + 2 >>> type(z) 42

>>>

>>> type(z) 52

Nó sẽ trả về một bộ, trong đó phần tử đầu tiên là bán kính và phần tử thứ hai là góc tính bằng radian. Lưu ý rằng bán kính có cùng giá trị với độ lớn, bạn hoàn toàn có thể tính giá trị này bằng phương pháp gọi _____266 trên số phức của tớ. trái lại, nếu bạn chỉ quan tâm đến góc của một số trong những phức, thì bạn hoàn toàn có thể gọi

>>> z = 3 + 2 >>> type(z) 44

>>>

>>> type(z) 53

Góc hoàn toàn có thể thu được bằng phương pháp sử dụng lượng giác cơ bản vì phần thực, phần ảo và độ lớn cùng nhau tạo thành một tam giác vuông

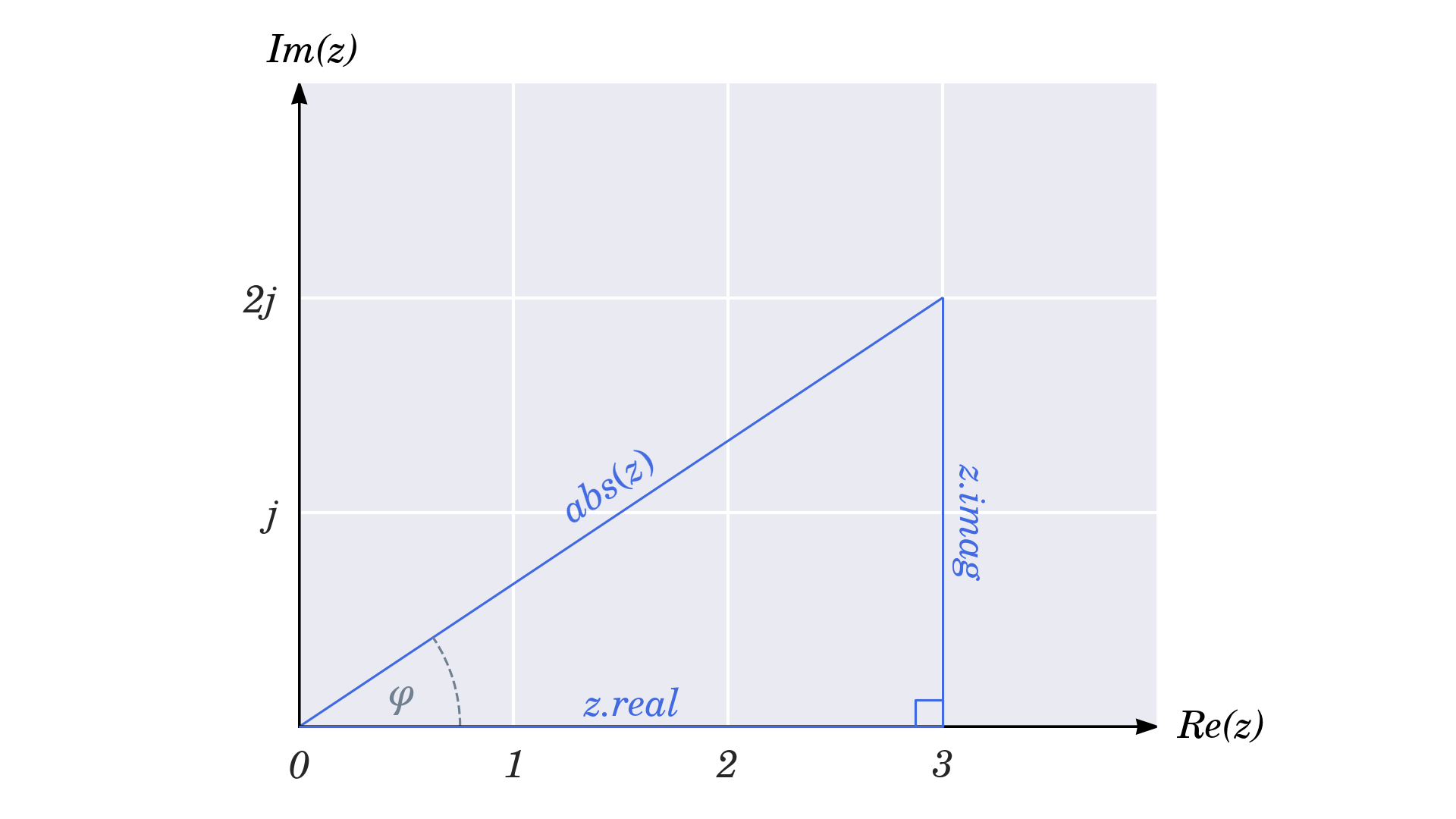
Bạn hoàn toàn có thể sử dụng những hàm lượng giác nghịch đảo, ví dụ như arcsine, từ

>>> type(z) 61 hoặc >>> z = 3.14 + 0j >>> type(z) 9, nhưng hàm sau sẽ tạo ra những giá trị phức tạp với phần ảo bằng 0

>>>

>>> type(z) 54

Có một rõ ràng nhỏ cần thận trọng khi sử dụng hàm arctangent, khiến nhiều ngôn từ lập trình phát triển một triển khai thay thế mang tên là ________ 447. Việc tính toán tỷ lệ giữa phần ảo và phần thực đôi khi hoàn toàn có thể tạo ra một điểm kỳ dị do, ví dụ, phép chia cho 0. Hơn nữa, những tín hiệu riêng của hai giá trị bị mất trong quá trình, làm cho việc xác định góc một cách chắc như đinh là không thể.

>>>

>>> type(z) 55

Lưu ý cách

>>> z = 3 + 2 >>> type(z) 48 không sở hữu và nhận ra hai điểm rất khác nhau nằm ở góc phần tư đối diện của hệ tọa độ. Mặt khác, >>> z = 3 + 2 >>> type(z) 47 mong đợi hai đối số thay vì một đối số để bảo toàn những tín hiệu riêng lẻ trước khi chia lẫn nhau và cũng tránh những vấn đề khác

Để lấy độ thay vì radian, bạn hoàn toàn có thể thực hiện lại quy đổi thiết yếu bằng mô-đun

>>> type(z) 61

>>>

>>> type(z) 56

Đảo ngược quy trình—nghĩa là quy đổi tọa độ cực thành tọa độ vuông góc—nhờ vào một hiệu suất cao khác. Tuy nhiên, bạn không thể chuyển cùng một bộ tài liệu mà bạn đã nhận được từ

>>> z = 3 + 2 >>> type(z) 42 vì >>> z = 3 + 2 >>> type(z) 52 mong đợi hai đối số riêng biệt

>>>

>>> type(z) 57

Bạn nên giải nén bộ tài liệu trước khi thực hiện một trách nhiệm và đặt tên mô tả cho những phần tử đó. Bây giờ bạn hoàn toàn có thể gọi đúng chuẩn

>>> z = 3 + 2 >>> type(z) 52

>>>

>>> type(z) 58

Bạn hoàn toàn có thể gặp phải những lỗi làm tròn trong khi Python thực hiện những phép tính. Đằng sau hậu trường, nó gọi những hàm lượng giác để lấy phần thực và phần ảo

>>>

>>> type(z) 59

Một lần nữa, việc bạn sử dụng

>>> type(z) 61 hay >>> z = 3.14 + 0j >>> type(z) 9 trong trường hợp này sẽ không quan trọng vì kết quả sẽ giống hệt nhau

Loại bỏ những quảng cáo

Biểu diễn số phức theo cách khác

Bất kể hệ tọa độ là gì, bạn hoàn toàn có thể màn biểu diễn cùng một số trong những phức trong một vài dạng tương đương về mặt toán học

Đại số (tiêu chuẩn)hình họclượng giácsố mũ

Danh sách này sẽ không đầy đủ vì có nhiều màn biểu diễn hơn, ví dụ như số phức

Có sự lựa chọn được cho phép bạn chọn một cách thuận tiện nhất để xử lý và xử lý một vấn đề nhất định. Ví dụ: bạn sẽ cần dạng hàm mũ để tính biến hóa Fourier rời rạc trong phần sắp tới. Sử dụng dạng này cũng phù phù phù hợp với phép nhân và phép chia số phức

Dưới đây là tóm tắt nhanh về những dạng số phức riêng lẻ và tọa độ của chúng

FormHình chữ nhậtCựcĐại sốz = x + y

>>> 2 + 3j + 4 + 5j (6+8j) 0-Hình họcz = (x, y)z = (r, φ)Lượng giácz =. z. (cos(x/. z. ) + >>> 2 + 3j + 4 + 5j (6+8j) 0sin(y/. z. ))z = r(cos(φ) + >>> 2 + 3j + 4 + 5j (6+8j) 0sin(φ))Số mũz =. z. e>>> z = 3 + 2 >>> type(z) 59z = r(e>>> 2 + 3j + 4 + 5j (6+8j) 0φ)

Dạng đại số có nguồn gốc từ Python khi bạn chỉ định những số phức bằng chữ của chúng. Bạn cũng hoàn toàn có thể xem chúng dưới dạng những điểm trên mặt phẳng Euclide trong hệ tọa độ Descartes hoặc cực. Mặc dù không còn màn biểu diễn riêng biệt cho dạng lượng giác hoặc hàm mũ trong Python, nhưng bạn hoàn toàn có thể xác minh xem những nguyên tắc toán học có đúng không

Ví dụ, thay công thức Euler về dạng lượng giác sẽ biến nó thành dạng mũ. Bạn hoàn toàn có thể gọi

>>> z = 3 + 2 >>> type(z) 62 của mô-đun >>> z = 3.14 + 0j >>> type(z) 9 hoặc nâng hằng số >>> z = 3 + 2 >>> type(z) 63 lên lũy thừa để đã có được kết quả tương tự

>>>

>>> type(z) 70

Tất cả những biểu mẫu thực sự là những cách rất khác nhau để mã hóa cùng một số trong những. Tuy nhiên, bạn không thể so sánh chúng trực tiếp do lỗi làm tròn số hoàn toàn có thể xảy ra trong thời gian chờ đón. Sử dụng

>>> z = 3 + 2 >>> type(z) 40 để so sánh bảo vệ an toàn và đáng tin cậy hoặc >>> z = 3 + 2 >>> type(z) 65 những số dưới dạng chuỗi một cách thích hợp. Bạn sẽ tìm hiểu cách định dạng những chuỗi như vậy trong phần sắp tới

Giải thích tại sao những dạng rất khác nhau của một số trong những phức lại tương đương nhau đòi hỏi phải tính toán và vượt xa phạm vi của hướng dẫn này. Tuy nhiên, nếu bạn quan tâm đến toán học, thì bạn sẽ thấy mối liên hệ Một trong những nghành toán học rất khác nhau được thể hiện bằng những số phức thật mê hoặc

Phân tích một số trong những phức trong Python

Bạn đã học được rất nhiều về số phức Python và đã xem những ví dụ sơ bộ. Tuy nhiên, trước khi tiếp tục, bạn nên đề cập đến một số trong những chủ đề ở đầu cuối. Trong phần này, bạn sẽ xem xét việc so sánh những số phức, định dạng những chuỗi chứa chúng, v.v.

Kiểm tra đẳng thức của số phức

Về mặt toán học, hai số phức bằng nhau khi chúng có những giá trị giống hệt nhau bất kể hệ tọa độ được sử dụng. Tuy nhiên, việc quy đổi giữa tọa độ cực và tọa độ hình chữ nhật thường gây ra lỗi làm tròn trong Python, vì vậy bạn cần để ý quan tâm đến những khác lạ nhỏ khi so sánh chúng

Ví dụ: khi bạn xem xét một điểm trên một đường tròn đơn vị có bán kính bằng 1 và nghiêng 60°, thì lượng giác hoạt động và sinh hoạt giải trí độc đáo, giúp việc quy đổi bằng bút và giấy trở nên đơn giản

>>>

>>> type(z) 71

Mặc dù bạn biết rằng

>>> z = 3 + 2 >>> type(z) 66 và >>> z = 3 + 2 >>> type(z) 67 giống nhau, nhưng Python không thể xác định điều đó do lỗi làm tròn. May mắn thay, tài liệu PEP 485 đã định nghĩa những hàm cho đẳng thức gần đúng, có sẵn trong những mô-đun >>> type(z) 61 và >>> z = 3.14 + 0j >>> type(z) 9

>>>

>>> type(z) 72

Hãy nhớ luôn sử dụng chúng khi so sánh những số phức. Nếu dung sai mặc định không đủ tốt cho những tính toán của bạn, bạn hoàn toàn có thể thay đổi nó bằng phương pháp chỉ định

Sắp xếp những số phức

Nếu bạn đã quen thuộc với những bộ tài liệu, thì bạn biết rằng Python hoàn toàn có thể sắp xếp chúng

>>>

>>> type(z) 73

Theo mặc định, những bộ tài liệu riêng lẻ được so sánh từ trái sang phải

>>>

>>> type(z) 74

Trong trường hợp đầu tiên, số

>>> z = 3 + 2 >>> type(z) 70 to hơn số >>> z = 3 + 2 >>> type(z) 71, vì vậy tên hành tinh hoàn toàn không được xem xét. Họ hoàn toàn có thể giúp xử lý và xử lý một sự ràng buộc, tuy nhiên. Tuy nhiên, đó không phải là trường hợp của số phức vì chúng không xác định quan hệ thứ tự tự nhiên. Ví dụ: bạn sẽ gặp lỗi nếu nỗ lực so sánh hai số phức

>>>

>>> type(z) 75

Kích thước tưởng tượng có nên nặng hơn kích thước thực không? . Vì bạn không thể so sánh trực tiếp những số phức, nên bạn cần cho Python biết phương pháp sắp xếp chúng bằng phương pháp chỉ định một hàm khóa tùy chỉnh, ví dụ như

>>> type(z) 66

>>>

>>> type(z) 76

Điều này sẽ sắp xếp những số phức theo độ lớn của chúng theo thứ tự giảm dần

Định dạng số phức dưới dạng chuỗi

Không có bất kỳ định dạng rõ ràng nào đối với số phức, nhưng bạn hoàn toàn có thể định dạng riêng phần thực và phần ảo của chúng bằng phương pháp sử dụng mã tiêu đúng cho số dấu phẩy động. Dưới đây, bạn sẽ tìm thấy một số trong những kỹ thuật chứng tỏ điều này. Một số trong số chúng sẽ thực sự áp dụng trình xác định định dạng của bạn cho tất cả phần thực và phần ảo trong một lần

Ghi chú. Định dạng chuỗi hoàn toàn có thể được cho phép bạn bỏ qua lỗi màn biểu diễn dấu phẩy động và vờ vịt như nó không tồn tại

>>>

>>> type(z) 77

Chữ cái

>>> z = 3 + 2 >>> type(z) 73 trong công cụ xác định định dạng là viết tắt của định dạng chung, làm tròn số của bạn đến độ đúng chuẩn được yêu cầu. Độ đúng chuẩn mặc định là sáu chữ số có nghĩa

Hãy lấy số phức sau đây làm ví dụ và định dạng nó bằng hai chữ số thập phân trên cả hai phần

>>>

>>> type(z) 78

Một cách nhanh gọn để thực hiện việc này là bằng phương pháp gọi

>>> z = 3 + 2 >>> type(z) 65 bằng một trình xác định định dạng số hoặc bằng phương pháp tạo một chuỗi f được định dạng phù hợp

>>>

>>> type(z) 79

Ví dụ: nếu bạn muốn trấn áp nhiều hơn nữa để thêm phần đệm tương hỗ update xung quanh toán tử dấu cộng, thì chuỗi f sẽ là lựa chọn tốt hơn

>>>

>>> z = 3.14 + 0j >>> type(z) 0

Bạn cũng hoàn toàn có thể gọi

>>> z = 3 + 2 >>> type(z) 75 trên một đối tượng chuỗi và truyền những đối số vị trí hoặc từ khóa cho nó

>>>

>>> z = 3.14 + 0j >>> type(z) 1

Các đối số vị trí đáp ứng một chuỗi những giá trị, trong khi những đối số từ khóa được cho phép bạn gọi chúng theo tên. Tương tự, bạn hoàn toàn có thể sử dụng (

>>> z = 3 + 2 >>> type(z) 76) với bộ tài liệu hoặc từ điển

>>>

>>> z = 3.14 + 0j >>> type(z) 2

Tuy nhiên, điều này sử dụng một cú pháp giữ nơi khác và hơi lỗi thời

Tạo kiểu tài liệu phức tạp của riêng bạn

Mô hình tài liệu Python định nghĩa một tập hợp những phương thức đặc biệt mà bạn hoàn toàn có thể triển khai để làm cho những lớp của bạn tương thích với một số trong những kiểu dựng sẵn nhất định. Giả sử bạn đang thao tác với những điểm và vectơ và muốn lấy góc giữa hai vectơ link. Bạn hoàn toàn có thể tính tích vô vị trí hướng của tớ và thực hiện một số trong những phép đo lượng giác. Ngoài ra, bạn hoàn toàn có thể tận dụng những số phức

Trước tiên hãy xác định những lớp của bạn

>>> z = 3.14 + 0j >>> type(z) 3

Một

>>> z = 3 + 2 >>> type(z) 77 có tọa độ >>> type(z) 14 và >>> type(z) 15, trong khi một >>> z = 3 + 2 >>> type(z) 80 nối hai điểm. Bạn hoàn toàn có thể nhớ >>> z = 3 + 2 >>> type(z) 44, tính toán khoảng chừng cách góc của một số trong những phức. Bây giờ, nếu bạn coi những vectơ của tớ là số phức và biết pha của chúng, thì bạn hoàn toàn có thể trừ chúng để đã có được góc mong ước

Để làm cho Python nhận ra những trường hợp vectơ dưới dạng số phức, bạn phải đáp ứng

>>> z = 3 + 2 >>> type(z) 82 trong phần thân của lớp

>>> z = 3.14 + 0j >>> type(z) 4

Mã bên trong phải luôn trả về một phiên bản của kiểu tài liệu

>>> type(z) 17, do đó, mã này thường tạo một số trong những phức mới từ đối tượng của bạn. Ở đây, bạn đang trừ điểm đầu và điểm cuối để đã có được những chuyển vị ngang và dọc, đóng vai trò là phần thực và phần ảo. Phương thức này sẽ chạy thông qua ủy quyền khi bạn gọi toàn cầu >>> type(z) 11 trên một phiên bản véc-tơ

>>>

>>> z = 3.14 + 0j >>> type(z) 5

Trong một số trong những trường hợp, bạn tránh việc phải tự đúc kiểu này. Hãy xem một ví dụ trong thực tế

>>>

>>> z = 3.14 + 0j >>> type(z) 6

Bạn có hai vectơ được xác định bởi bốn điểm phân biệt. Tiếp theo, bạn chuyển chúng trực tiếp tới

>>> z = 3 + 2 >>> type(z) 44, thực hiện quy đổi thành số phức cho bạn và trả về pha. Độ lệch pha là góc giữa hai vectơ

Điều đó không đẹp sao?

Tính phép biến hóa Fourier rời rạc với số phức

Mặc dù bạn hoàn toàn có thể sử dụng những số thực để tính thông số sin và cosin của tần số của một hàm tuần hoàn với biến hóa Fourier, nhưng sẽ thuận tiện hơn nếu chỉ xử lý một thông số phức trên mỗi tần số. Biến đổi Fourier rời rạc trong miền phức tạp được cho bởi công thức sau

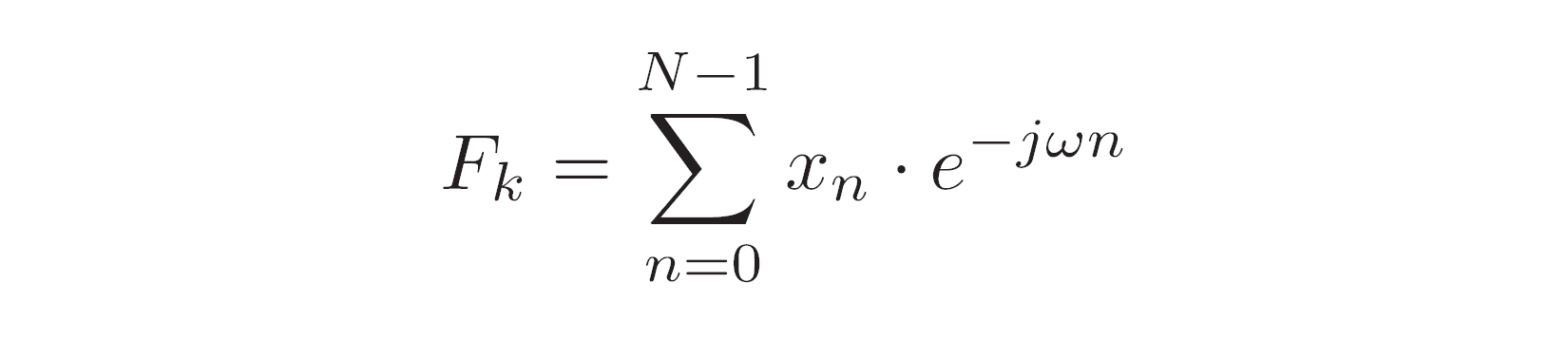
Đối với mỗi ngăn tần số k, nó đo lường mối tương quan của tín hiệu và một sóng hình sin rõ ràng được biểu thị dưới dạng số phức ở dạng hàm mũ. (Cảm ơn Leonhard Euler. ) Tần số góc của sóng hoàn toàn có thể được tính bằng phương pháp nhân góc tròn là 2π radian với k trên số mẫu rời rạc

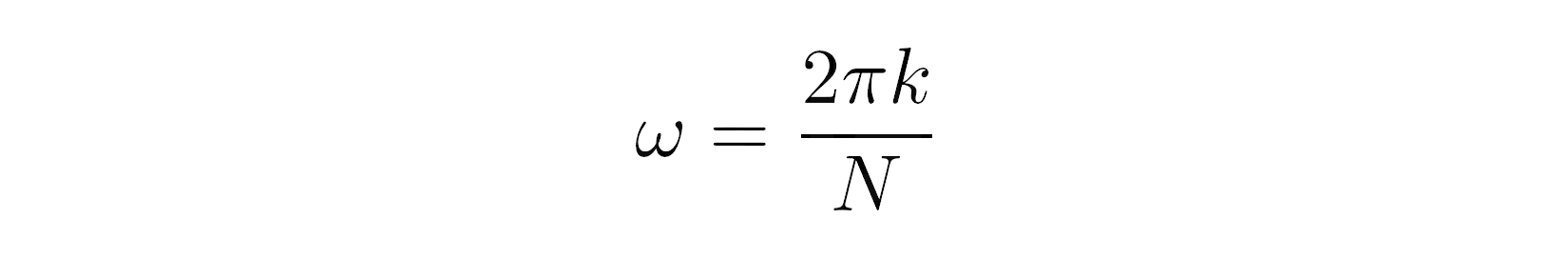
Viết mã này bằng Python trông khá ngăn nắp khi bạn tận dụng kiểu tài liệu

>>> type(z) 17

>>> z = 3.14 + 0j >>> type(z) 7

Hàm này là phiên âm theo nghĩa đen của những công thức trên. Giờ đây, bạn hoàn toàn có thể chạy phân tích tần số trên âm thanh mà bạn tải từ tệp âm thanh bằng mô-đun

>>> z = 3 + 2 >>> type(z) 87 của Python hoặc bạn tổng hợp từ đầu. Một trong những Máy tính xách tay Jupyter đi kèm với hướng dẫn này được cho phép bạn chơi với tổng hợp và phân tích âm thanh một cách tương tác

Để vẽ phổ tần số bằng Matplotlib, bạn phải biết tần số lấy mẫu, tần số này xác định độ phân giải của ngăn tần số cũng như số lượng giới hạn Nyquist

>>> z = 3.14 + 0j >>> type(z) 8

Số lượng ngăn tần số trong quang phổ bằng một nửa số mẫu, trong khi tần số Nyquist số lượng giới hạn tần số cao nhất bạn hoàn toàn có thể đo được. Biến đổi trả về một số trong những phức có độ lớn tương ứng với biên độ của sóng hình sin ở tần số đã cho, trong khi góc của nó là pha

Ghi chú. Để đã có được những giá trị biên độ đúng chuẩn, bạn phải nhân đôi số và chia độ lớn kết quả cho số lượng mẫu. Mặt khác, nếu bạn chỉ quan tâm đến biểu đồ tần số, thì bạn hoàn toàn có thể chuẩn hóa độ lớn theo tổng của chúng hoặc tần số tối đa

Đây là biểu đồ tần số mẫu của sóng âm gồm có ba âm—440 Hz, 1. 5 kHz và 5 kHz—có biên độ bằng nhau

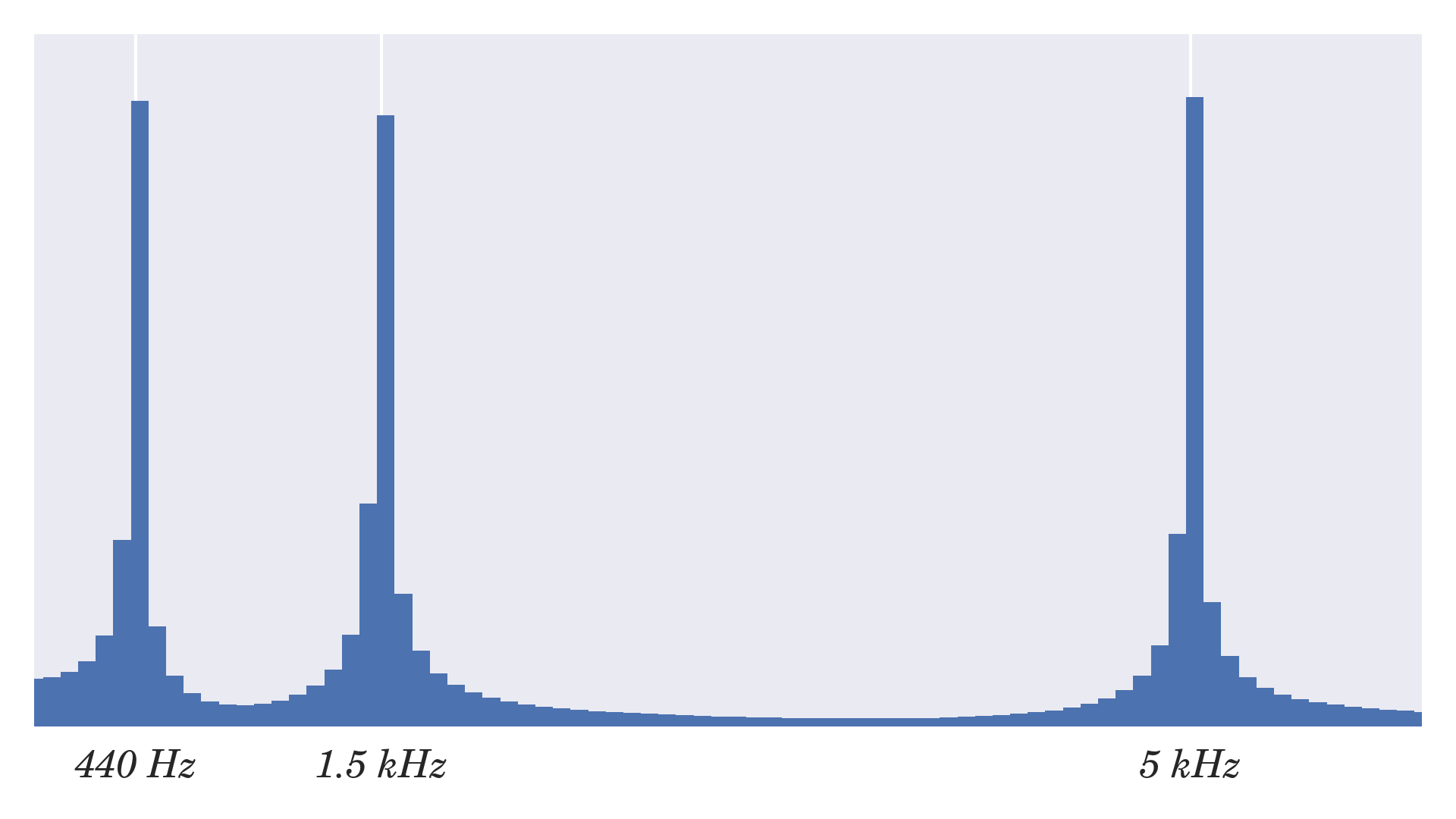Biểu đồ phổ tần số

Lưu ý rằng đây là một ví dụ hoàn toàn mang tính chất chất học thuật vì việc tính toán biến hóa Fourier rời rạc với những phép lặp lồng nhau có O(n2) , khiến nó không thể sử dụng được trong thực tế. Đối với những ứng dụng thực tế, bạn muốn sử dụng thuật toán biến hóa Fourier nhanh (FFT) được triển khai tốt nhất trong thư viện C, ví dụ như FFT trong SciPy

Phần kết luận

Việc thuận tiện và đơn giản sử dụng những số phức trong Python khiến chúng trở thành một công cụ thiết thực và thú vị một cách đáng ngạc nhiên. Bạn đã thấy những vectơ hai chiều được triển khai thực tế miễn phí và bạn hoàn toàn có thể phân tích tần số âm thanh nhờ chúng. Các số phức được cho phép bạn diễn đạt những công thức toán học trong mã một cách tao nhã mà không cần nhiều cú pháp soạn sẵn cản trở

Trong hướng dẫn này, bạn đã học cách

Xác định số phức bằng chữ trong PythonBiểu diễn những số phức trong hệ tọa độ vuông góc và cựcSử dụng số phức trong biểu thức số họcTận dụng mô-đun >>> z = 3.14 + 0j >>> type(z) 9 tích hợpDịch những công thức toán học trực tiếp sang mã Python

Cho đến nay, trải nghiệm của bạn với số phức Python là gì?

Bạn hoàn toàn có thể nhấp vào link phía dưới để lấy mã nguồn đầy đủ cho hướng dẫn này

Nhận mã mẫu. Nhấp vào đây để lấy mã mẫu mà bạn sẽ sử dụng để tìm hiểu về số phức trong Python trong hướng dẫn này

Đánh dấu là đã hoàn thành xong

🐍 Thủ thuật Python 💌

Nhận một Thủ thuật Python ngắn và mê hoặc được gửi đến hộp thư đến của bạn vài ngày một lần. Không có thư rác bao giờ. Hủy đăng ký bất thần. Được quản lý bởi nhóm Real Python

Gửi cho tôi thủ thuật Python »

Giới thiệu về Bartosz Zaczyński

Bartosz là người hướng dẫn bootcamp, tác giả và lập trình viên đa ngôn từ yêu thích Python. Anh ấy giúp sinh viên của tớ tiếp cận công nghệ tiên tiến phần mềm bằng phương pháp chia sẻ kinh nghiệm tay nghề thương mại hơn một thập kỷ trong ngành CNTT

» tin tức thêm về Bartosz

Mỗi hướng dẫn tại Real Python được tạo bởi một nhóm những nhà phát triển để nó đáp ứng những tiêu chuẩn rất chất lượng của chúng tôi. Các thành viên trong nhóm đã thao tác trong hướng dẫn này là

Aldren

David

Geir Arne

Joanna

Gia-cốp

Bậc thầy Kỹ năng Python trong thế giới thực Với quyền truy cập không số lượng giới hạn vào Python thực

Tham gia với chúng tôi và có quyền truy cập vào hàng nghìn hướng dẫn, khóa học video thực hành và hiệp hội những Pythonistas Chuyên Viên

Nâng cao kỹ năng Python của bạn »

Bậc thầy Kỹ năng Python trong thế giới thực
Với quyền truy cập không số lượng giới hạn vào Python thực

Tham gia với chúng tôi và có quyền truy cập vào Hàng trăm hướng dẫn, khóa học video thực hành và hiệp hội Pythonistas Chuyên Viên

Nâng cao kỹ năng Python của bạn »

Bạn nghĩ sao?

Đánh giá nội dung bài viết này

Tweet Chia sẻ Chia sẻ E-Mail

Bài học số 1 hoặc điều yêu thích mà bạn đã học được là gì?

Mẹo phản hồi. Những nhận xét hữu ích nhất là những nhận xét được viết với mục tiêu học hỏi hoặc giúp sức những sinh viên khác. và nhận câu vấn đáp cho những thắc mắc phổ biến trong cổng thông tin tương hỗ của chúng tôi

Tải thêm tài liệu liên quan đến nội dung bài viết Số ảo python programming python

Video Số ảo python ?

Bạn vừa Read tài liệu Với Một số hướng dẫn một cách rõ ràng hơn về Review Số ảo python tiên tiến nhất

Chia Sẻ Link Download Số ảo python miễn phí

Bạn đang tìm một số trong những Share Link Down Số ảo python miễn phí.

Thảo Luận thắc mắc về Số ảo python

Nếu sau khi đọc nội dung bài viết Số ảo python vẫn chưa hiểu thì hoàn toàn có thể lại Comment ở cuối bài để Mình lý giải và hướng dẫn lại nha #Số #ảo #python